Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 39

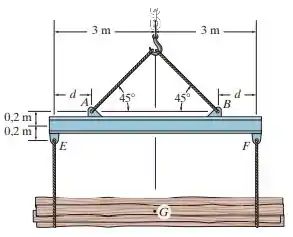
A viga de elevação é usada para o manuseio de materiais. Se a carga suspensa tem peso de 2   k N e centro de gravidade em G , determine a posição d dos suportes no topo da viga, de modo que não haja momento fletor desenvolvido dentro da extensão A B da viga. Os cabos de amarração são compostos de duas pernas posicionadas a 45 ° , como mostra a figura.

Passo 1

Fala, galera do RespondeAí. Beleza? Bora para mais um exercício de Mecânica. Primeiro, vamos determinar as reações nos suportes. Temos:

∑ M E = 0 F E 6 - 2 3 = 0 F E = 1   k N

E também:

∑ F y = 0 F F + 1 - 2 = 0 F F = 1   K N

Pela tração da corda, temos:

∑ F x = 0 F A C cos ⁡ 45 ° - F B C cos ⁡ 45 ° = 0 F A C = F B C = F

Já para o eixo y , temos:

∑ F y = 0 2 F sin ⁡ 45 ° - 1 - 1 = 0 F A C = F B C = 1,414   k N

Passo 2

Por fim, vamos fazer a análise das forças internas. Esse problema requer que o momento no ponto H   é M H = 0 . Com isso, temos que:

∑ M H = 0 1 d + x - 1,414 sin ⁡ 45 °   0,2 = 0 d = 0,200   m

Opa, é isso, galera. Bora praticar mais!!!

Resposta

d = 0,200   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o esforço cortante e o momento fletor como uma função de x , e depois construa os diagramas de esforço cortante e de momento fletor.
Determine o esforço cortante e o momento fletor como uma função de x , e depois construa os diagramas de esforço cortante e de momento fletor.
Determine o esforço cortante e o momento fletor como uma função de x , e depois construa os diagramas de esforço cortante e de momento fletor.
Determine as forças internas (força axial, esforço cortante e momento fletor) no ponto J das estruturas indicadas.Estrutura e carregamento do Problema 6.79 .
Determine as forças internas (força axial, esforço cortante e momento fletor) no ponto J das estruturas indicadas.Estrutura e carregamento do Problema 6 . 80 .