Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas fundamentais - Ex. 10
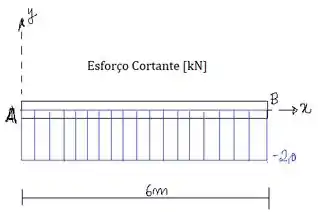
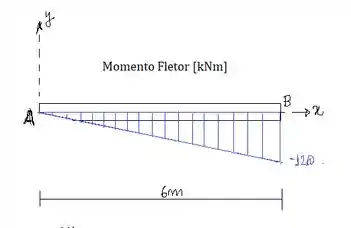
Determine o esforço cortante e o momento fletor como uma função de , e depois construa os diagramas de esforço cortante e de momento fletor.
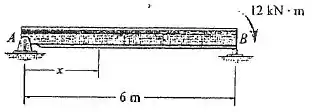
Passo 1
Vamos desenhar o diagrama de corpo livre da viga, beleza?
Antes de determinarmos o esforço cortante e o momento fletor, vamos encontrar as forças de reação a partir do diagrama de corpo livre acima. Para um sistema em equilíbrio, o somatório dos momentos e forças deve ser igual a zero. Assim,
Passo 2
Vamos olhar para a porção que compreende o intervalor . Vamos aplicar as equações de equilíbrio no diagrama de corpo livre para determinarmos a força cortante e o momento fletor .
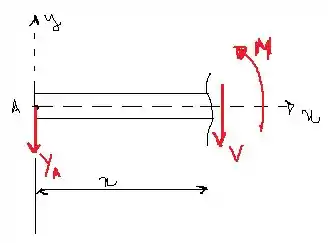
Passo 3
Vamos agora plotar os diagramas de esforço cortante e momento fletor. A função de esforço cortante é constante ao longo da viga, com valor máximo de:
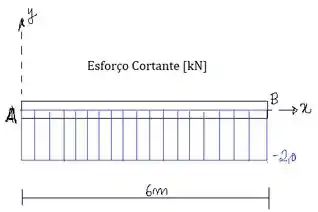
A função do momento fletor atinge seu valor máximo no ponto também:
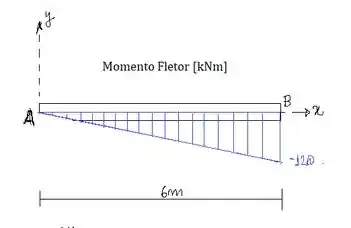
Resposta
