Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 68

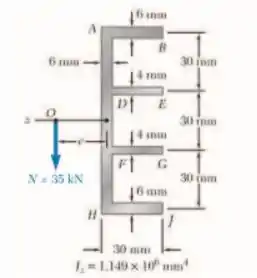
Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante vertical V aplicada em O.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo: Começaremos esboçando o diagrama de corpo livre e posteriormente a inércia, vem comigo :D

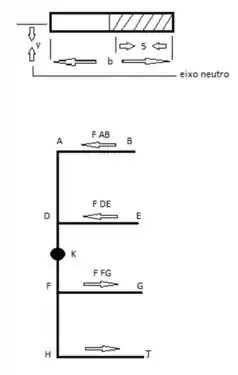
Calculando a inércia temos:

I A B = I H J = 1 12 30 6 3 + 30 6 ( 45 ) 2 = 0,365 × 10 6 m m 4

I D E = I F G = 1 12 30 4 3 + 30 4 ( 15 ) 2 = 0,02716 × 10 6 m m 4

I A H = 1 12 6 90 3 = 0,3645 × 10 6 m m 4

A inércia total é dada por:

I = Σ I = 1,14882 × 10 6 m m 4

Passo 2

Agora vamos responder a alternativa A, partiu :D

(a) Para um flange típico,

A s = t s

Q s = y t s

q s = V Q s I = V y t s I

F =   ∫ 0 b q s d s = V y t b 2 2 I

Para o Flange AB:

F A B = V 45 ( 6 ) ( 30 ² ) ( 2 ) ( 1,14882 × 10 6 = 0,10576 V ⟵

Para o Flange DE:

F D E = V 15 ( 4 ) ( 30 ² ) ( 2 ) ( 1,14882 × 10 6 ) = 0,023502 V ⟵

Para o Flange FG:

F F G = 0,023502 V →

Para o Flange HJ:

F H J = 0,10576 V →

Vamos determinar o momento e por fim teremos a resposta de A , UFAAA!!!

+ ↺ Σ M K = + ↺ Σ M K : V e = 45 F A B + 15 F D E + 15 F F G + 45 F H J = 10,223 V

Dividindo por V, e = 10,22   m m

Passo 3

Agora vamos responder a alternativa B, partiu :D

(b) Calculando a tensão de cisalhamento trazemos os dados abaixo ;)

V = 35 × 10 3 N                               I = 1,14882 × 10 - 6 m 4

Em B, E, G, e J, τ = 0

Em A e H,

Q = 30 6 45 = 8,1 × 10 3 m m 3 = 8,1 × 10 - 6   m ³

t = 6 × 10 - 3   m

Então teremos a tensão de cisalhamento ;)

τ = V Q I t = 35 × 10 3 ( 8,1 × 10 - 6 ) ( 1,14882 × 10 - 6 ) ( 6 × 10 - 3 ) = 41,1 × 10 6 P a = 41,1   M P a

Logo acima de D e logo abaixo de F:

Q = 8,1 × 10 3 + 6 30 30 = 13,5 × 10 3 m m 3 = 13,5 × 10 - 6 m ³

Considerando: t = 6 × 10 - 3 m

τ = V Q I t = 35 × 10 3 ( 13,5 × 10 - 6 ) ( 1,14882 × 10 - 6 ) ( 6 × 10 - 3 ) = 68,5 × 10 6 P a = 68,5   M P a

Logo a direita de D e logo a direita de F:

Q = 30 4 15 = 1,8   × 10 3 m m ³ = 1,8   × 10 - 6   m 3         t = 4   × 10 - 3   m

τ = V Q I t = 35 × 10 3 ( 1,8 × 10 - 6 ) ( 1,14882 × 10 - 6 ) ( 4 × 10 - 3 ) = 13,71 × 10 6 P a = 13,71   M P a

Passo 4

Logo abaixo de D e logo acima de F:

Q = 13,5 × 10 3 + 1,8 × 10 - 6 = 15,3 × 10 3 m m 3 = 15,3 × 10 - 6 m ³

Considere: t = 6 × 10 - 3 m

τ = V Q I t = 35 × 10 3 ( 15,3 × 10 - 6 ) ( 1,14882 × 10 - 6 ) ( 6 × 10 - 3 ) = 77,7 × 10 6 P a =   77,7   M P a

Em K,

Q = 15,3 × 10 3 + 6 15 7,5 = 15,975 × 10 3 m m 3 = 15,975 × 10 - 6 m ³

τ = V Q I t = 35 × 10 3 ( 15,975 × 10 - 6 ) ( 1,14882 × 10 - 6 ) ( 6 × 10 - 3 ) = 81,1 × 10 6 P a =   81,1   M P a

Resposta

  1. 10,22   m m
  2. 41,1   M P a , 68,5   M P a , 13,71   M P a , 77,7   M P a , 81,1   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de aço ( E = 210G P a ) e uma barra de alumínio ( E = 70 G P a ) são unidas para formar a barra composta mostrada na figura. Determine a tensão máxima.No alumínio No aço Quando a barra é fle
Uma viga de madeira de 152,4m mx304,8m m foi reforçada aparafusando-se nela o reforço de aço mostrado na figura. O modulo de elasticidade para a madeira é de 12,4G P a , e para o aço de 200G P a . Sab
Para a barra composta indicada, determine o raio de curvatura provocado pelo momento fletor 200N m
Uma barra de aço ( E = 210G P a ) e uma barra de alumínio ( E = 70 G P a ) são unidas para formar a barra composta mostrada na figura. Determine a tensão máxima.No alumínio No aço Quando a barra é fle
Uma viga de madeira de 152,4m mx304,8m m foi reforçada aparafusando-se nela o reforço de aço mostrado na figura. O modulo de elasticidade para a madeira é de 12,4G P a , e para o aço de 200G P a . Sab