Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 82

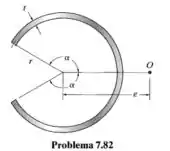
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura.

Passo 1

Como nas demais questões de fluxo de cisalhamento, o procedimento de resolução consiste em integrar o fluxo de cisalhamento sobre a seção para encontrar a força interna e calcular o somatório de momentos.

As dificuldades nessa questão são de não conhecermos uma forma fácil de calcular as propriedades geométricas (momento de inércia e momento estático). Para resolver isso vamos utilizar coordenadas polares e integrar ao longo da seção.

Outra dificuldade é saber onde será o ponto de aplicação da força encontrada. Porém, isso na verdade não importa! Pois a força obrigatoriamente estará sobre a parede fina. Então se fizermos o somatório de momentos em relação ao centro C , o braço do momento será igual ao raio, e não precisaremos nos importar em descobrir o ponto exato em que a força atua.

Passo 2

Observe o elemento infinitesimal θ .

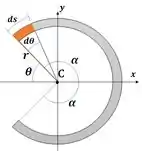
O momento de inércia de um corpo é dado por:

d I = y 2 d A

No nosso caso:

y = r ⋅ sen ⁡ θ

d A = t ⋅ d s = t ⋅ r ⋅ d θ

Dessa forma:

d I = r 2 ⋅ sen 2 ⁡ θ ⋅ t ⋅ r ⋅ d θ

Aplicamos a integração. Os limites foram definidos dessa forma evitar que eles se anulem.

I = r 3 t ∫ π - α π + α sin 2 ⁡ θ d θ  

Lembrando das tabelas de integrais temos:

I = r 3 t ⋅ 1 2 ⋅ θ - 1 4 sen ⁡ 2 θ π - α π + α  

Resolvendo:

I = r 3 t ⋅ 1 2 π + α - π + α - 1 4 ( sen ⁡ 2 π + 2 α - sen ⁡ 2 π - 2 α )

I = r 3 t ⋅ α - 1 4 ( sen ⁡ 2 α - sen ⁡ - 2 α )

I = r 3 t ⋅ α - 1 4 ( sen ⁡ 2 α + sen ⁡ 2 α )

I = r 3 t ⋅ α - sen ⁡ 2 α 2

Chegamos na expressão para o momento de inércia:

I = r 3 t 2 ⋅ 2 α - sen ⁡ 2 α

Passo 3

Agora vamos calcular o momento estático. Como será preciso integrar o momento estático para determinar a força, vamos determinar uma fórmula pro momento estático.

O momento estático é definido como:

d Q = y d A

No nosso caso:

y = r ⋅ sen ⁡ θ

d A = t ⋅ d s = t ⋅ r ⋅ d θ

Então:

d Q = r ⋅ sen ⁡ θ ⋅ t ⋅ r ⋅ d θ

d Q = r 2 t ⋅ sen ⁡ θ ⋅ d θ

Vamos efetuar a integração. Os limites são definidos do ponto inicial π - α , até um ponto θ qualquer.

Q = r 2 t ∫ π - α θ sen ⁡ θ d θ  

Q = r 2 t - cos ⁡ θ π - α θ  

Q = r 2 t ⋅ ( - cos ⁡ θ + cos ⁡ π - α )  

Q = r 2 t ⋅ ( - cos ⁡ θ - cos ⁡ α )  

Chegamos numa fórmula pro momento estático.

Q = - r 2 t ⋅ ( cos ⁡ θ + cos ⁡ α )  

Passo 4

Agora que temos o momento estático e de inércia, podemos integrar o fluxo de cisalhamento ao longo do caminho d s para determinar a força que atua sobre a seção.

F = ∫ q d s

Substituindo a fórmula do momento estático:

F = ∫ V Q I ⋅ d s

Substituindo o d s = r d θ

F = ∫ V Q I ⋅ r d θ

A força cortante é igual a força aplicada: V = P

F = ∫ P Q r I ⋅ d θ

Vamos definir os limites de ponta a ponta da seção, da mesma forma que fizemos com o momento de inércia:

F = P r I ∫ π - α π + α - r 2 t ⋅ ( cos ⁡ θ + cos ⁡ α ) d θ  

F = - r 3 t ⋅ P I ∫ π - α π + α ( cos ⁡ θ + cos ⁡ α ) d θ  

F = - r 3 t ⋅ P I ⋅ sen ⁡ θ - θ ⋅ cos ⁡ α π - α π + α  

F = - r 3 t P I ⋅ sen ⁡ ( π + α ) - sen ⁡ π - α - ( π + α ) ⋅ cos ⁡ α + ( π - α ) ⋅ cos ⁡ α  

F = - r 3 t P I ⋅ - 2 sen ⁡ ( α ) - 2 α ⋅ cos ⁡ α  

F = r 3 t P I ⋅ 2 sen ⁡ ( α ) + 2 α ⋅ cos ⁡ α  

Substituindo o momento de inércia:

F = r 3 t P r 3 t 2 ⋅ 2 α - sen ⁡ 2 α ⋅ 2 sen ⁡ ( α ) + 2 α ⋅ cos ⁡ α  

Chegamos numa expressão para a força.

F = 4 P 2 α - sen ⁡ 2 α ⋅ sen ⁡ α + α ⋅ cos ⁡ α  

Passo 5

Agora efetuamos o somatório de momentos sobre o ponto C, pois apesar de não termos definido em que ponto a força F atua, sabemos que ela fica sobre a seção. E qualquer ponto da seção está a uma distância r do ponto C .

∑ M C = 0 ⇒ P ⋅ e - F ⋅ r = 0

P e = F r

e = 1 P ⋅ 4 P 2 α - sen ⁡ 2 α sen ⁡ α + α ⋅ cos ⁡ α ⋅ r

e = 4 r sen ⁡ α + α ⋅ cos ⁡ α 2 α - sen ⁡ 2 α

Resposta

e = 4 r sen ⁡ α + α ⋅ cos ⁡ α 2 α - sen ⁡ 2 α

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas peças de madeira de 80x120mm, de seção transversal retangular e uniforme, são unidas por simples colagem das seções chanfradas, como mostrado. Sabendo-se que as máximas tensões admissíveis na jun
Um tubo de aço de 300mm de diâmetro externo é fabricado com chapa fina de 6,35mm de espessura, soldada ao longo de uma hélice que forma um ângulo de 22,5 graus com um plano perpendicular ao eixo do tu
As seções transversais de duas vigas extrudadas, cada uma com espessura da parede uniforme e igual a 6,35 m m são mostradas. Para uma força cortante vertical de 11120N , determinar a máxima tensão de
Para a viga de seção transversal mostrada, submetida a uma força cortante vertical de 25k N , determinar a tensão de cisalhamento, quando d = 50 m m , no:Ponto b
Para a viga de seção transversal mostrada, submetida a uma força cortante vertical de 25k N , determinar a tensão de cisalhamento, quando d = 50 m m , no:Ponto a