Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 83
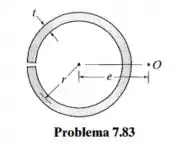
Determine a localização do centro de cisalhamento (ponto O) para o tubo que tem uma fenda ao longo de seu comprimento
Passo 1
É uma questão de fluxo de cisalhamento, então o procedimento de resolução consiste em integrar o fluxo de cisalhamento sobre a seção para encontrar a força interna e calcular o somatório de momentos!
As dificuldades nessa questão são:
- não conhecermos uma forma fácil de calcular o momento de inércia
- não conhecermos uma forma fácil de calcular momento estático.
Para contornar isso vamos utilizar coordenadas polares e integrar ao longo da seção.
OBS: Esta questão é muito semelhante a questão 7.82. Inclusive, se você definir o , na questão anterior, você terá a mesma relação pro momento de inércia e pro momento estático.
Passo 2
Observe o elemento infinitesimal .
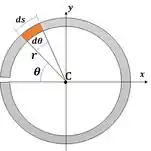
O momento de inércia de um corpo é dado por:
No nosso caso:
Dessa forma:
Aplicamos a integração:
Pelas identidades trigonométricas:
Integrando:
Chegamos na expressão do momento de inércia:
Passo 3
Agora vamos calcular o momento estático. Como será preciso integrar o momento estático para determinar a força, vamos determinar uma fórmula pro momento estático.
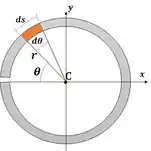
O momento estático é definido como:
No nosso caso:
Então:
Vamos efetuar a integração. Os limites são definidos do ponto inicial , até um ponto qualquer.
Chegamos numa fórmula pro momento estático.
Passo 4
Agora que temos o momento estático e de inércia, podemos integrar o fluxo de cisalhamento ao longo do caminho para determinar a força que atua sobre a seção.
Substituindo a fórmula do momento estático:
Substituindo o
A força cortante é igual a força aplicada:
Vamos definir os limites de ponta a ponta da seção, da mesma forma que fizemos com o momento de inércia:
Efetuando a integração:
Substituindo o momento de inércia:
A força é:
Resposta
Passo 5
Agora efetuamos o somatório de momentos sobre o ponto C, pois apesar de não termos definido em que ponto a força atua, sabemos que ela fica sobre a seção. E qualquer ponto da seção está a uma distância do ponto .
