Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 32b
Uma viga extrudada tem a seção transversal mostrada e está submetida a uma força cortante vertical de 45kN. Para t= 6,3mm, determinar a tensão de cisalhamento no: (b) ponto b
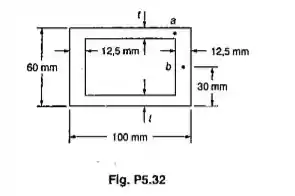
Passo 1
Precisamos calcular o momento de inércia:
Vamos agora calcular o momento estático para encontrar a tensão no ponto B. Perceba que o ponto B se encontra exatamente no meio da seção transversal, nesse caso é legal desenhar uma linha horizontal e separar a seção em dois trechos.
Com isso podemos calcular o momento estático:
Passo 2
Com isso o fluxo de cisalhamento é:
Como desenhado na figura, a linha horizontal corta B e B’, isso mostra que o fluxo de cisalhamento naquele ponto é dividido por 2.
A tensão de cisalhamento será então:
Resposta
(b)
Exercícios de Livros Relacionados
Selecione no apêndice B a viga de abas largas de aço que tenha o menor peso e que suportará com segurança as cargas mostradas. A tensão de flexão admissível é σ = 160M P a e a tensão de cisalhamento a
A viga afunilada simplesmente apoiada suporta a força concentrada p em seu centro. Determine a tensão de flexão máxima absoluta na viga.
A viga mostrada na figura suporta uma carga distribuída uniforme w. Se for feita de uma chapa com largura constante b, determine a tensão de flexão máxima absoluta na viga.
As polias acopladas ao eixo estão carregadas como mostra a figura. Se os mancais em A e B exercem somente forças horizontais e verticais sobre o eixo, determine, com aproximação de 1m m , o diâmetro e
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60M P a , determine, com aproximação de 1m m , o eixo de menor diâmetro que suportará a carga. Use a teoria