Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 32a
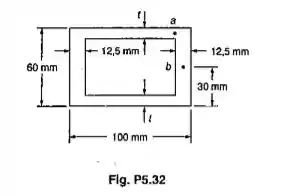
Uma viga extrudada tem a seção transversal mostrada e está submetida a uma força cortante vertical de 45kN. Para t= 6,3mm, determinar a tensão de cisalhamento no: (a) ponto a
Passo 1
Precisamos calcular o momento de inércia:
Vamos agora calcular o momento estático para encontrar a tensão no ponto A. Lembrando que nesses casos é sempre bom pensar no fluxo de cisalhamento, que se divide em partes iguais se o trecho for simétrico. Então vamos criar um ponto a’ que seja simétrico ao ponto a e separar esse trecho da viga.
O momento estático do trecho será:
Passo 2
Com isso o fluxo de cisalhamento é:
Porém como dito antes, o fluxo se divide de forma igual para a e a’, assim:
A tensão de cisalhamento será então:
Resposta
Exercícios de Livros Relacionados
A largura das abas da viga é b = 200m m . Se a tensão de flexão máxima não puder ultrapassar σ a d m = 160M P a , determine o maior peso da máquina que a viga pode suportar. O centro de gravidade da m
A viga foi construída com tábuas como mostra a figura. Se cada prego puder suportar uma força de cisalhamento de 1k N , determine o espaçamento máximo entre os pregos s, s’, s’’ com aproximação de 25
Determine a variação na altura d de uma em balanço que suporta uma força concentrada P em extremidade, de modo que ela tenha uma tensão de flexão máxima constante σ a d m em todo o seu comprimento. A
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e