Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 42
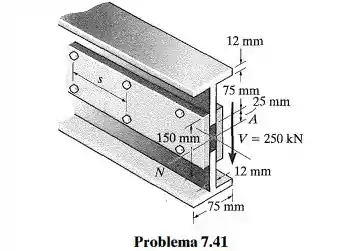
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de e espessura de . Se os parafusos estiverem espaçados de , determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN
Passo 1
Fala galerinha bonita, tudo beleza?
Saca só, se a gente pegar a vista frontal e colocar do lado da vista lateral, vamos ver algo mais ou menos assim:
Como podemos notar, a seção transversal é perfeitamente simétrica, o que garante que o centroide é no meio da figura!
Então vamos calcular o momento de inércia em relação ao centroide.
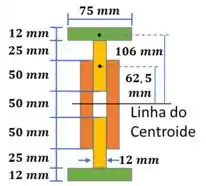
Podemos escrever o momento inércia da seguinte forma:
Lembrando que:
E pelo teorema dos eixos paralelos que será aplicado para as figuras em verde e laranja a gente precisa ainda fazer o seguinte.
Onde d é a distância de um eixo até o outro e A é a área da peça, no nosso caso eles estão distando em y e o teorema dos eixos paralelos será aplicado para Ix.
Passo 2
Mostrado o nosso objetivo vamos então aos cálculos, fechado? Vamos começar pelo momento de inércia da peça verde, como são duas e são simétricas:
Substituindo temos:
Faremos o mesmo processo para as peças amarelas.
Substituindo os valores da figura.
Por ultimo mas não menos importante, as peças laranjas podemos calcular sem a necessidade de aplicar o teorema dos eixos paralelos.
Agora a gente parte pro momento estático.
Precisamos selecionar uma região que começa numa das extremidades da viga, e vá até a região de contato do parafuso!
Nesse caso, a melhor área é a destacada em laranja.
Lembre-se, para calcular o momento estático, vamos multiplicar o a área vezes o centroide, e somar as regiões:
Substituindo os valores da figura a gente tem.
Determinamos a parte da geometria, agora vamos para os esforços.
Passo 3
Agora vamos calcular a força cisalhante .
Mas primeiro, precisamos saber: “De que forma o parafuso resiste ao fluxo de cisalhamento?”
Observe a figura abaixo:
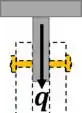
Note que o parafuso, destacado em amarelo, está sofrendo um cisalhamento duplo gerado pelo fluxo .
O número dois aparece na equação abaixo pois o fluxo gera um cisalhamento duplo.
Sabemos que o fluxo de cisalhamento é dado pela equação . Vamos aplicar isso:
Isolando
Lembrando que o enunciado nos diz que :
E
E os outros valores foram previamente calculados.
Logo: