Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 74

Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .

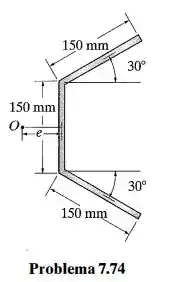
Passo 1

Dados da questão: d = 150   m m

A questão pede: e = ?

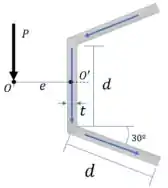
Vamos calcular a força que atua na aba inclinada, depois vamos utilizar o somatório de momentos em O ' para calcular a distância e .

Para isso vamos precisar calcular o momento de inércia da seção e desenvolver uma fórmula que represente o momento estático.

Passo 2

Para facilitar o cálculo do momento de inércia, vamos definir:

d 2 = d ⋅ s e n 30 = d 2

t 2 = t s e n ⁡ 30 = 2 t

I = 2 t 2 d 2 3 12 + t 2 d 2 d + d 2 2 2 + t d 3 12

I = 2 2 t ⋅ d 2 3 12 + 2 t ⋅ d 2 ⋅ d + d 2 2 2 + t d 3 12

I = 4218750 ⋅ t

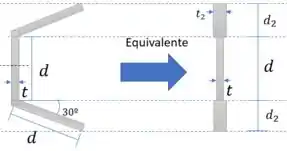
Passo 3

Agora vamos determinar a força que atua nas abas. Primeiro precisamos calcular uma função para o momento estático:

Q = x 1 t ⋅ d 2 + d s e n 30 - x 1 s e n 30 2

Q = x 1 t ⋅ d 2 + d 2 - x 1 4

Q = x 1 t ⋅ d - x 1 4

Q = d ⋅ x 1 t - 1 4 x 1 2 t

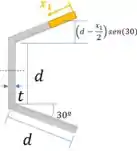
Chegamos numa expressão para o momento estático:

Q = 1 4 4 ⋅ d ⋅ x 1 t - x 1 2 t

Passo 4

Vamos calcular a força gerada pelo fluxo de cisalhamento na aba. Para encontrar a força sobre a aba basta integrar o fluxo de cisalhamento:

F 1 = ∫ 0 d q ⋅ d x  

F 1 = ∫ 0 d V Q I ⋅ d x  

A força cortante é igual à força aplicada V = P

F 1 = ∫ 0 d P Q I ⋅ d x  

F 1 = P I ∫ 0 d Q ⋅ d x

Substituindo o momento estático  

F 1 = P t 4 I ∫ 0 d 4 ⋅ d ⋅ x 1 - x 1 2 ⋅ d x

Efetuando a integração:

F 1 = P t 4 I 4 ⋅ d ⋅ x 1 2 2 - x 1 3 3 0 d

F 1 = 5 ⋅ d 3 P t 12 I

Substituindo os valores:

F 1 = 5 ⋅ 150 3 12 ( 4218750 ⋅ t ) P t

F 1 = P 3

Passo 5

Agora vamos calcular o somatório de momentos em O '

∑ M O ' = 0 ⇒ - 2 F ⋅ c o s 30 ⋅ d + P ⋅ e = 0

P ⋅ e = F ⋅ c o s 30 ⋅ d

Substituindo os valores

P ⋅ e = P 3 ⋅ 3 2 ⋅ 150

e = 3 6 ⋅ 150

e = 43,30   m m

Resposta

e = 43,30   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indi
Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indi
Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensã
A seção transversal de uma viga extrudada é uma seção quadrada vazada de lado a = 75m m e espessura t = 6,35m m . Para uma força cortante vertical 65k N , determinar a máxima tensão de cisalhamento na
Para uma viga feita de dois ou mais materiais com diferentes módulos de elasticidade, mostra que a Eq. 510 τ = V Q I t Permanece válida, desde que os valores de Q e I sejam calculados usando a seção t