Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 63
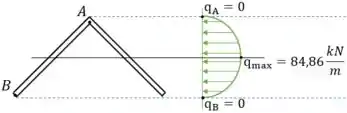
A cantoneira está sujeita a um cisalhamento . Faça um rascunho da distribuição do fluxo de cisalhamento ao longo da aba AB. Indique valores numéricos em todos os picos.
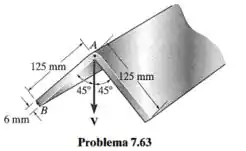
Passo 1
Dados da questão:
A questão pede a distribuição de cisalhamento na aba AB.
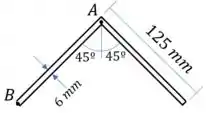
Estratégia de resolução: Vamos calcular o centroide e o momento de inércia e depois o fluxo de cisalhamento na aba AB.
Passo 2
Encontrar o centroide da seção parece complicado. Mas se lembrarmos da fórmula do momento de inércia, vamos perceber que a inclinação não faz diferença. A única coisa que nos interessa é a base e a altura da estrutura. Então temos uma equivalência como mostrado abaixo. Uma barra inclinada é equivalente a uma barra reta de mesma altura
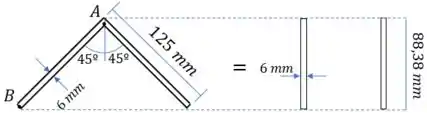
Dessa forma, tal qual uma barra, o centroide é na metade da altura:
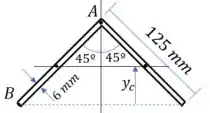
Passo 3
O momento de inércia segue o mesmo raciocínio. Então basta calcular o momento de inércia correspondente a duas barras.
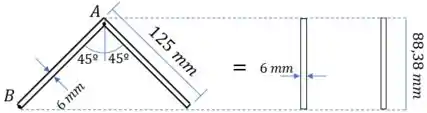
Passo 4
O cálculo do momento estático será da mesma forma. Como nosso interesse é a distribuição de tensão, precisamos calcular o momento estático máximo:
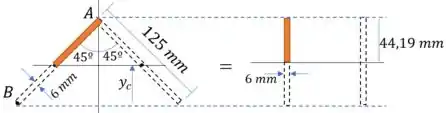
Passo 5
Agora podemos calcular o momento estático máximo
Convertendo a unidade:
Passo 6
Para fazer a distribuição de tensão basta lembrar que:
- A tensão de cisalhamento em uma ponta é igual a zero
- A tensão tem comportamento parabólico
