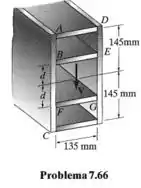
A força de cisalhamento é aplicada à viga-mestra-caixão. Determine a posição das chapas de reforço e de modo que o fluxo de cisalhamento em seja duas vezes maior do que o fluxo de cisalhamento em . Use as dimensões da linha central para o cálculo. Todas as chapas tem de espessura.
Passo 1
Dados da questão:
A questão pede a distância máxima para
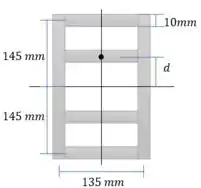
Estratégia de resolução: A figura é perfeitamente simétrica, e por isso seu centroide já é definido. Depois calcularemos os Momentos Estáticos de A e B em função de . Por fim utilizando a relação podemos determinar o valor de
Um erro comum nessa questão é tentar calcular o momento de inércia, o que deixa a questão desnecessariamente complexa. Perceba que quando igualarmos poderemos cortar o momento de inércia dos dois lados, e por isso NÃO é preciso calcular o momento de inércia.
Passo 2
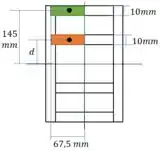
Agora vamos calcular os momentos estáticos:
Passo 3
A questão nos afirma que:
Substituindo a equação do momento estático
Simplificando:
Substituindo: