Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 3

7.3. Determine as forças internas no ponto J quando α = 90 °

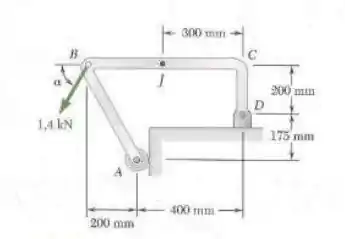
Passo 1

Vamos começar desenhando a situação

Vamos usar o momento para descobrir algumas coisas importantes

∑ M D = 0

1,4 ⋅ 0,6 - A x ⋅ 0,175 = 0

Então

A = A x = 4,8   k N

E agora vamos tratar toda imagem como um corpo livre

∑ F x = 0

D x - 4,8 = 0

Então

D x = 4,8   k N

E depois

∑ F y = 0

D y - 1,4 = 0

Logo

D y = 1,4   k N

Passo 2

Agora para achar as forças que precisamos a gente tem que usar o corpo livre em J C D -

Onde F é a força axial, V é o esforço cortante e M o momento fletor.

Agora é só usar as equações de equilíbrio

∑ F x = 0

4,8 - F = 0

Logo

F = 4,8   k N

∑ F y = 0

1,4   k N - V = 0

Logo

V = 1,4   k N

E finalmente

∑ M j = 0

4,8 ⋅ 0,2 + 1,4 ⋅ 0,3 - M = 0

Logo

M = 1,38   k N ⋅ m

Resposta

F = 4,8   k N

V = 1,4   k N

M = 1,38   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força normal interna, o esforço cortante e o momento nos pontos C e D da viga. O ponto D está localizado à direita da carga de 25k N .
Determine a força normal interna, o esforço cortante e o momento atuando no ponto C , e também no ponto D , que está localizado à direita do apoio de rolete em B .
Determine a força normal interna, o esforço cortante e o momento nos pontos C e D da viga simplesmente apoiada. O ponto D está localizado à esquerda da força de 5k N .
Determine a distância a em termos da dimensão L da viga entre os apoios A e B simetricamente posicionados de modo que o momento interno no centro da viga seja zero.
Determine a força normal interna, o esforço cortante e o momento nos pontos D e E nos dois membros.