Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 172
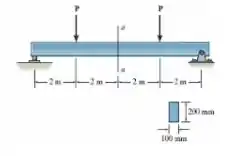
A viga é feita de um material elástico plástico para o qual σe = 200 MPa. Se o maior momento na viga ocorre no interior da seção central a-a, determine o valor de cada força P que faz com que esse momento seja (a) o maior momento elástico e (b) o maior momento plástico.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga tem uma esse formato de um retângulo, e nos pede a força máxima para encontrar os maiores momentos. Partiu??
Passo 2
Ok, nós vamos começar pensando na barra. Vamos achar quanto vale cada uma das reações de apoio e o momento máximo visto pela viga.
Feito isso, vamos achar a distância d através das nossas forças de contração e de tração. Sabendo disso, vamos calcular nosso C1 (T1) inicial.
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos o nosso momento.