Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 181

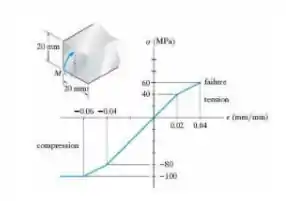
A barra de plexiglass tem uma curva tensão – deformação que pode ser aproximada pelos segmentos de reta mostrados na figura. Determine o maior momento M que pode ser aplicado à barra antes que ela falhe.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga tem uma esse formato de um quadradinho, e nos pede o momento para que ela não falhe, ou seja, a tensão desse momento deve ser igual à admissível. Partiu??

Passo 2

Ok, nós vamos começar pensando na barra. Vamos achar quanto vale a nossa deformação e a nossa tensão máximas, ok??

ε 0,02 - 0,010334 =   0,04 0,010334

ε = 0,037417   m m / m m

σ 0,037417 =   804 0,04

σ = 74,833   M P a

Pronto, com as nossas tensão e deformação encontradas, vamos achar nossas forças de contração e as de tração.

C = 74,833 10 6 0,5   0,02 - 0,010334 0,02 = 7233,59   N  

T 1 = 0,5 100   x   10 6 0,02 0,010334 0,5 = 5166,85   N

T 2 = 40   x   10 6   0,5   0,02 0,010334 0,5 = 2066,74   N

y c = 6,442   m m

y 1 = 3,445   m m

y 2 = 7,9225   m m

Passo 3

Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos o nosso momento.

M = 2 ∫ y σ d A

M = 94,7   N . m

Resposta

M = 94,7   N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga-caixão é feita de um material elástico perfeitamente plástico para o qual σe = 250 MPa. Determine a tensão residual nas partes superior e inferior da viga após a aplicação e posterior remoção d
A viga é feita de um material elástico perfeitamente plástico. Determine o momento plástico Mp que pode ser suportado por uma viga que tenha a seção transversal mostrado na figura σe = 210 MPa.
A haste tem seção transversal circular. Se for feita de um material elástico plástico, determine o fator de forma e o módulo de seção plástica Z.
A viga curva está sujeita a um momento fletor M = 900 N.m como mostra a figura. Determine a tensão nos pontos A e B e mostre a tensão sobre um elemento de volume localizado em cada desses pontos.
Em voo, a nervura curva do avião a jato é submetida a um momento previsto M = 16 N.m na seção. Determine a tensão de flexão máxima na nervura nessa seção e trace um rascunho bidimensional da distribui