A viga na na Figura 6.54f é submetida a um momento totalmente plástico Mp. Prove que as tensões de cisalhamento longitudinal e transversal na viga são nulas. Dica: Considere um elemento da viga como mostra a Figura 7.4d.

Imagine a distribuição de tensão sobre os dois lados da seção de uma viga:

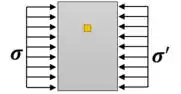
A seção está sobre comportamente completemente plástico. A tensão sobre ela será constante ao longo de toda a seção transversal e será igual a tensão de escoamento

Observe o pequeno elemento infinitesimal qualquer destacado em amarelo. Se estudarmos este elemento teremos:

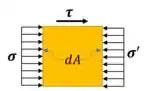
Se multiplicarmos as tensões pelas áreas termos forças:

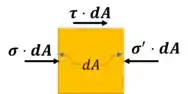
Como a viga é estática, então a soma das forças em qualquer elemento deve ser estática também. Então vamos aplicar a equação de equilíbrio em

Observe, contudo, que , então:

Concluímos então que: Em uma região sobre tensão plástica não há tensão de cisalhamento, uma vez que as tensões normais sobre todos os lados de um elemento infinitesimal são iguais.