Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 87
Para a viga indicada, um momento igual ao momento de plastificação é aplicado e, em seguida, removido. Usando uma tensão de escoamento de , determine a tensão residual em .
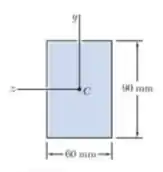
Passo 1
Para determinação no momento plástico, consideramos a seção inteiramente plastificada, ou seja, podemos definir a seguinte seção:
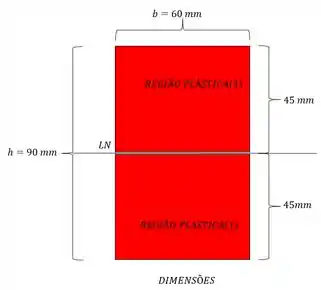
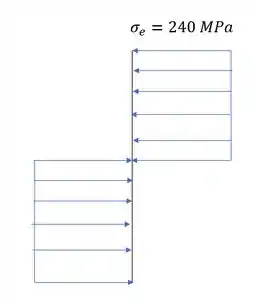
E sabemos que a região plástica, nada mais é que a região onde a tensão de escoamento é constante, ou seja, podemos fazer o seguinte diagrama:
Sabemos que a força é determinada por:
Passo 2
Sabemos que a equação de tensão é dada por:
Agora pensa no seguinte, sabemos que o momento máximo que age na nossa seção é dado pelo momento plástico, assim, temos que:
O ponto que queremos saber o que ocorre é o dado por:
Assim o nosso momento de inércia vai ser dado por:
Assim temos que:
Substituindo na nossa equação teremos que:
Agora pensa no seguinte, o nosso diagrama de tensão máxima atuante na nossa seção é dado por:
E pensa no seguinte, qual a máxima tensão que a nossa estrutura suporta, se desenhássemos o diagrama, ela seria dada por:
O seja, se fizermos um diagrama menos o outro temos o diagrama de tensões residuais em todos os pontos da viga, porém, pensa no seguinte, o enunciado só pediu a tensão residual APENAS, no ponto , assim, temos que a tensão residual é dada por.