Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 136

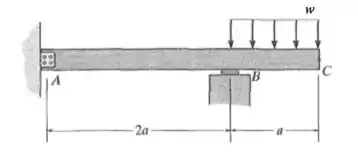
A viga de madeira está sujeita à carga mostrada na figura. Considere que o apoio em A é um pino e em B, um rolete. Determine a inclinação em A e o deslocamento em C. Use o teorema dos momentos de área. EI é constante. Pela função de Macaulay

Passo 1

Fala aí pessoal, partiu mais um problema de resmat. Este problema pede as reações de apoio e os diagramas. Primeiro, vamos fazer o DCL:

Passo 2

Primeiro, vamos calcular a reação nos apoios:

∑ M A = 0 2 a B y - w a 5 a 2 = 0 B y = 5 w a 4

∑ F y = 0 - A y + B y - w a = 0 A y = 5 w a 4 - w a A y = w a 4

Passo 3

Pela função de Maculay:

M x = - w a 4 x + 5 w a 4 < x - 2 a > 1 - w 2 < x - 2 a > 2

E I d 2 v d x 2 = M x = - w a 4 x + 5 w a 4 < x - 2 a > 1 - w 2 < x - 2 a > 2

E I d v d x = - w a 8 x 2 + 5 w a 8 < x - 2 a > 2 - w 6 < x - 2 a > 3 + C 1 E I v = - w a 24 x 3 + 5 w a 2 4 < x - 2 a > 3 - w 24 < x - 2 a > 4 + C 1 x + C 2

Passo 4

Com isso, temos as condições de contorno. São elas:

x = 0 x = 2 a → v = 0

Substituindo as condições de contorno na equação, temos: C 1 = w a 3 6

C 2 = 0

Passo 5

Por fim, a inclinação em A ocorre em x = 0 . Sendo assim:

θ A = w a 3 6 E I

E o deslocamento, também ocorre em x = 0 . Por isso:

∆ C = 11 w a 4 24 E I

Resposta

θ A = w a 3 6 E I

∆ C = 11 w a 4 24 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que a viga AD é feita de uma barra de aço com seção transversal cheia, determine (a) a inclinação no ponto B e (b) a deflexão no ponto A. Use E = 200 GPa.
Para a viga e o carregamento mostrados na figura, determine (a) a inclinação no ponto C e (b) a deflexão no ponto D. Use E = 200 GPa.
Para a viga e o carregamento mostrados na figura, determine (a) a inclinação na extremidade A, (b) a inclinação na extremidade B e (c) a deflexão no ponto médio C.
Para a viga e o carregamento mostrados na figura, determine a intensidade e localização da maior deflexão para baixo. Viga e carregamento do Problema 9.126.
Para a viga e o carregamento mostrados na figura, determine a deflexão (a) no ponto D e (b) no ponto E.