Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 83
Para a viga mostrada, determine a reação em .
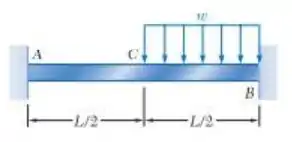
Passo 1
Fala aí, galera. Tudo beleza? Vamos fazer mais uma questão pra tirar aquele notão na prova.
Para determinarmos as reações em e , temos que dividir esta viga em casos de superposição. Neste caso, serão dois tipos de carregamento.
Primeiro, temos que o carregamento vai ser aplicado ao segmento da viga e corresponde aos caso e do apêndice . Portanto, podemos escrevêlos como uma soma e, assim, a deflexão no ponto vai ser:
Já para a inclinação no mesmo ponto, temos:
O carregamento corresponde aos caso e . Para a deflexão no ponto , temos:
E para a inclinação no mesmo ponto, temos:
Agora que conseguimos todos os carregamentos de superposição, vamos determinar as reações.
Passo 2
Então, agora que encontramos a deflexão e a inclinação para cada caso de superposição, vamos utilizar a deflexão no ponto , que é e é dada pela soma das deflexões dos dois casos de superposição. Portanto:
E para a inclinação em , temos:
Opa, com isso ficamos com um sistema de duas equações e duas incógnitas. Vamos adiantar o seu lado resolvendo este sisteminha. Assim, ficamos com:
Passo 3
Agora que determinamos as reações em , vamos utilizar as equações de equilíbrio no segmento para determinarmos as reações restantes. Temos:
E também:
Mais uma questão resolvida, galera! Bora fazer mais?.