Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 66

Para a viga em balanço e o carregamento mostrados na figura, determine a inclinação e a deflexão na extremidade livre.

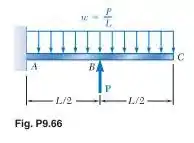
Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Neste caso, usaremos as fórmulas do apêndice 2 do capítulo. Separaremos os carregamentos e faremos a superposição. Considerando apenas a carga distribuída e usando o apêndice para a parte A C :

θ C ' = - P L L 3 6 E I = - 1 6 P L 2 E I

y C ' = - P L L 4 8 E I = - 1 8 P L 3 E I

Agora, vamos considerar apenas o esforço aplicado. Para a parte A B , usando o apêndice:

θ B ' ' = P L 2 2 2 E I = 1 8 P L 2 E I

y B ' ' = P L 2 3 3 E I = 1 24 P L 3 E I

Para a parte B C :

θ C ' ' = θ B ' ' = 1 8 P L 2 E I

y C ' ' = y B ' ' + L 2   θ B ' ' = 1 24 P L 3 E I + 1 16 P L 3 E I = 5 48 P L 3 E I

Passo 2

Agora, basta usar a superposição de efeitos. Logo:

θ C = θ C ' + θ C ' '

y C = y C ' + y C ' '

Substituindo pelas fórmulas encontradas acima e somando as parcelas, teremos:

θ C = P L 2 24 E I

y C = P L 3 48 E I

Prontinho, mais uma questão feita!

Resposta

θ C = P L 2 24 E I

y C = P L 3 48 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga em balanço e o carregamento mostrados na figura, determine (a) a inclinação e (b) a deflexão no ponto A.
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A e (b) a deflexão no centro C da viga.
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A e (b) a deflexão no centro C da viga.
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A e (b) a deflexão no centro C da viga.
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A e (b) a deflexão no centro C da viga.