Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 84
Para a viga prismática mostrada, determine a deflexão no ponto
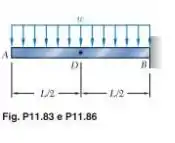
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Primeiramente, sabemos que a energia de deformação é dada por:
A deflexão é dada por:
Na parte
Para
Fazendo e substituindo na integral:
Resposta
Exercícios de Livros Relacionados
Um bloco C de 11,5k g move-se horizontalmente com uma velocidade v 0 até chocar-se com a coluna A B , como mostrado. Usando E = 200G P a , determinar a maior velocidade v 0 , para que a tensão normal
Resolver o Prob. 10.66, assumindo que a coluna A B foi girada de 90 ° , em torno do eixo longitudinal.
Um tubo de alumínio com a seção transversal mostrada sofre em sua seção média o impacto de um bloco de 6k g , que se move na horizontal com uma velocidade de 2m / s . Usando E = 70G P a , determinar:a
O bloco D de 20k g é abandonado de uma altura h = 180m m , acima da viga de aço A B . sabendo-se que E = 200G P a , determinar:a máxima deflexão no ponto E ;a máxima tensão na viga.
Resolver o Prob. 10.62, assumindo-se que ambas as porções da barra A B C são feitas de bronze.