Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 133a
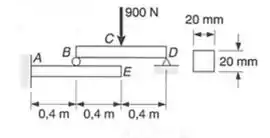
A viga BD repousa sobre a viga em balanço AE, como mostrado. Sabendo-se que uma barra quadrada de lado é usado para cada uma das vigas, determinar a deflexão, para o carregamento indicado, no:
- Ponto C . Usar
Passo 1
Fala galera, esse problema é bem interessante, ele pode parecer algo muito complexo, mas ele é bem de boas. Até aqui sempre consideramos a deformação nos apoios igual a zero, mas nesse caso, como o ponto B está acima de outra viga, o nosso apoio em B também vai deformar, e com isso, teremos que somar essas duas deformações, então para isso, vamos fazer o seguinte, em um primeiro momento, vamos determinar a deformação em C e as reações de apoio da viga BCD, e assim, vamos ter a seguinte figa a ser analisada:
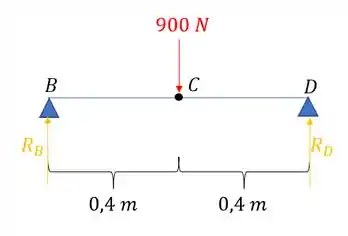
A fórmula da deformação é dada por:
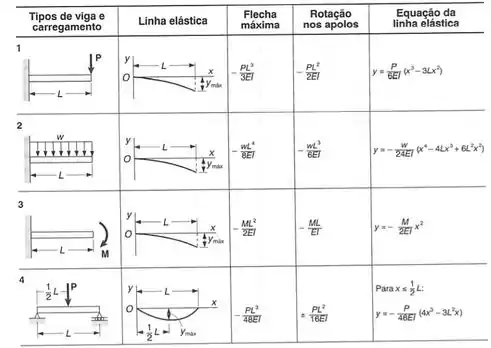
Assim a deformação é dada por:
Sabemos que:
E a inércia é dada por:
Assim a deformação em C é dada por:
E as reações de apoio são dadas por:
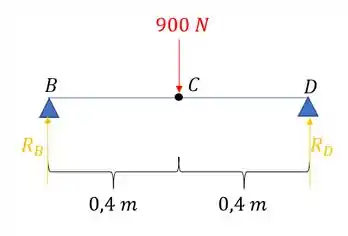
Passo 2
Agora que temos a reação, podemos transferir a carga no ponto B para a barra de baixo, e basta determinarmos a deformação na barra de baixo no ponto B, porque ai vamos ter quando o apoio em B caiu, assim, temos que:
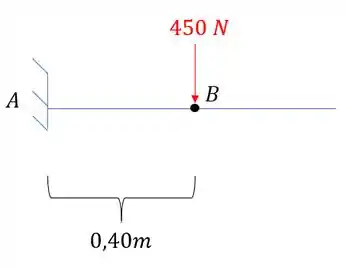
A fórmula da deformação é dada por:
Considerando a carga em B como sendo o fim do engaste, teremos que a deformação em B vai ser dada por:
Sabemos que:
E a inércia no fim da tabela é dada por:
Assim a deformação em b é dada por:
Como para o ponto B a deformação está acontecendo no apoio, para termos quanto ela contribui par a deformação em C, precisamos fazer a seguinte relação:
Assim a deformação total em C, é dada por: