Para a viga com o carregamento mostrado, determinar:
- A Deflexão no ponto B. usar
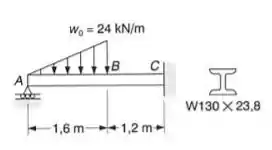
Passo 1
Sabemos pelo item a) que as nossas equações singulares para deformações e deflexões são dadas por:
E sabemos que usando as seguintes equações de equilíbrio:

Obtemos o seguinte sistema:
Resolvendo o nosso sistema, temos que:
E assim a nossa equação passa a ser:
Para determinarmos , precisamos dos dados que obtemos na tabela no fim do livro, assim temos que:
Substituindo na nossa equação, temos que:
Os termos que dão zero e que dá negativo dentro dos parênteses, podemos ignorar, porque pelas nossas equações singulares, esses termos podem ser ignorados:
Resposta
b)