Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 159

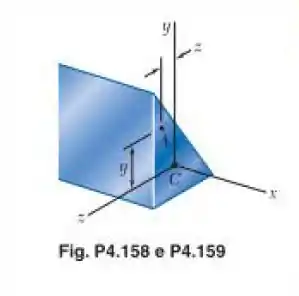
Uma viga de seção transversal assimétrica está submetida a um momento M 0 atuando no plano vertical x y . Mostre que a tensão no ponto A, de coordenadas y e z , é

σ A = - y I y - z I y z I y I z - I y z 2 M z

Em que I y , I z e I y z são os momentos e produto de inércia da seção transversal em relação aos eixos coordenados, e M z o momento fletor.

Passo 1

Beleza! Antes de começar, sabemos que a tensão no ponto A varia linearmente com as coordenadas y e z. Já que a força axial é zero, os eixos y e z são eixos centroidais. Dessa forma podemos escrever a tensão σ A como:

σ A = C 1 y + C 2 z

Sendo C 1 e C 2 constantes. Sabendo disso, podemos escrever o momento em torno do eixo z através da relação integral dada por:

M y = ∫ z σ A d A

Substituindo a relação encontrada para σ A , teremos:

M y = ∫ z C 1 y + C 2 z d A

Agora vamos separar essa integral em duas, chegando em:

M y = ∫ C 1 y z d A + ∫ C 2 z 2 d A → M y = C 1 ∫ y z d A + C 2 ∫ z 2 d A

Agora, nós sabemos o que representam essas duas integrais, são o produto de inércia com relação a yz e o momento de inércia com relação a y:

M y = C 1 I y z + C 2 I y

Já que o momento está sendo aplicado no plano xy, o momento M y será igual a zero. Dessa forma, a equação acima se torna:

0 = C 1 I y z + C 2 I y → C 2 I y = - C 1 I y z → C 2 = - C 1 I y z I y

Passo 2

Agora nós vamos calcular o momento em relação ao eixo z através da forma integral:

M z = - ∫ y σ A d A

Substituindo a relação encontrada para σ A , teremos:

M z = - ∫ y C 1 y + C 2 z d A

Separando em duas integrais, teremos:

M z = - C 1 ∫ y 2 d A - C 2 ∫ y z d A

Novamente, essas duas integrais serão o momento de inércia com relação a z e o produto de inércia com relação yz, então a equação acima se torna:

M z = - C 1 I z - C 2 I y z

Substituindo a expressão encontrada para C 2 na equação acima, teremos:

M z = - C 1 I z - - C 1 I y z I y I y z

Agora, manipulando essa equação para encontrar uma expressão para C 1 , chegamos em:

M z = - C 1 I z + C 1 I y z 2 I y → M z = C 1 - I z + I y z 2 I y

M z = C 1 - I z I y + I y z 2 I y → C 1 = M z I y I y z 2 - I z I y

Passo 3

Agora vamos substituir a expressão encontrada para C 1 na equação de C 2 , então teremos:

C 2 = - C 1 I y z I y = - M z I y I y z 2 - I z I y I y z I y → C 2 = - M z I y z I y z 2 - I z I y

Agora nós vamos substituir as expressões encontradas para C 1 e C 2 na equação que escrevemos para σ A lá no passo 1, então, teremos:

σ A = C 1 y + C 2 z = M z I y I y z 2 - I z I y y + - M z I y z I y z 2 - I z I y z

σ A = M z I y y I y z 2 - I z I y - M z I y z z I y z 2 - I z I y

Agora, como temos o mesmo denominador, podemos juntar os numeradores e escrever:

σ A = M z I y y - M z I y z z I y z 2 - I z I y

Colocando o termo M z em evidência, teremos:

σ A = M z I y y - I y z z I y z 2 - I z I y

Agora, trocando os sinais no numerador e no denominador (observe que estamos multiplicando a equação por -1 em cima e embaixo), chegamos na relação pedida no enunciado:

σ A = - M z I y y - I y z z I z I y - I y z 2

Pronto! Essa é a relação que queremos encontrar.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o gancho mostrado, determinar a maior tensão na seção a-a, quando b1 = 50 mm e b2 = 10 mm.
Mostrar que, se a seção transversal de uma viga curva consiste de dois ou mais retângulos, o raio R da superfície neutra pode ser expresso como:Onde A é a área total da seção transversal.
Usando a equação 4.66, desenvolva a expressão para R, da figura abaixo, para uma seção transversal triangular.
Sabendo-se que o semi-anel mostrado h=40 mm, determinar a tensão no ponto A e no ponto B.
Sabendo-se que o semi-anel mostrado h=30 mm, determinar a tensão no ponto A e no ponto B.