Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 156

Mostre que, se uma viga de seção retangular sólida é fletida por um momento aplicado no plano que contém a diagonal da seção transversal retangular, o eixo neutro repousará ao longo da outra diagonal.

Passo 1

Tá legal! Vamos começar desenhando os eixos y e z na viga em questão. E vamos desenhar o ângulo ϕ formado com o eixo neutro, dessa forma, teremos:

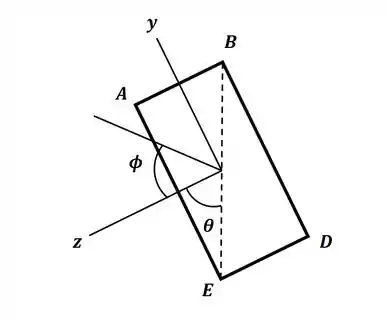
Então, temos que o ângulo formado entre a diagonal da seção transversal retangular e o eixo escolhido será:

t g   θ = b h

Passo 2

Agora vamos escrever os momentos de inércia para a viga com relação aos eixos y e z. Lembrando que como temos uma seção retangular, o momento de inércia é dado por:

I = a b 3 12

Onde temos que a é a medida do lado paralelo ao eixo do momento em que estamos calculando, e b é a medida do lado transversal. Então, no nosso caso, para o momento em y temos:

I y = h b 3 12

E, para o momento em z , teremos:

I z = b h 3 12

Passo 3

Agora, sabemos que o ângulo ϕ formado pelo eixo neutro pode ser encontrado através de:

t g   ϕ = I z I y t g   θ

Dessa forma, substituindo os valores encontrados nos passos anteriores, teremos:

t g   ϕ = b h 3 12 h b 3 12 b h → t g   ϕ = b h 3 12 12 h b 3 b h

Simplificando a expressão, chegamos em:

t g   ϕ = h 2 b 2 b h → t g   ϕ = h b

Dessa forma, podemos ver que o eixo neutro de fato passa pela outra diagonal da seção retangular.

Resposta

t g   ϕ = h b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra prismática AB é construída de uma liga de bronze para a qual a curva de tensão-deformação específica em tração é mostrada na figura. Considerando que a curva de σ em função de ϵ é a mesma em
Um pequeno bloco de mateira suporta uma carga axial de 27 kN, como indicado. Determine a tensão no ponto A quando: (a) b = 0; (b) b = 38 mm; (c) b = 76 mm.
Uma barra prismática de seção transversal retangular é feita por uma liga para a qual a curva tensão-deformação específica pode ser representada pela relação ϵ = k σ 3 . Se um momento fletor M é aplic
Duas forças de 10 kN são aplicadas a uma barra retangular de 20 mm × 60 mm, como mostrado. Determinar a tensãono ponto A, quando: (a) b = 0; (b) b = 15 mm; (c) b = 25 mm.
Qualquer dar três cargas axiais, de intensidade P = 45 kN podem ser aplicadas na extremidade de um perfil de aço laminado w200 × 31,3. Determinar a tensão no ponto A: (a) para o carregamento mostrado;