Uma viga com a seção transversal mostrada é feita de aço considerado elastoplástica com e . Um conjunto de flexão é aplicado à viga na direção do eixo , produzindo zonas plásticas com de espessura que se desenvolvem no topo e na base da viga. Depois de removido o conjugado, determine.
- a tensão residual em
- os pontos onde a tensão residual é zero.
- O raio de curvatura correspondente à deformação permanente da viga.
Nota do expert: o enunciado apresenta um equivoco quanto ao tamanho da região plástica, ela não possui uma espessura de , na verdade, ela se inicia no ponto , ou seja, a espessura da região plástica na verdade é de e não como o enunciado apresenta.
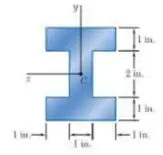
Passo 1
Sabemos pelo enunciado que os superiores e inferiores são a região plástica, significa que a tensão máxima que ela chega é a de escoamento, e entre as duas regiões de existe a região elástica, e na região elástica, o funcionamento das tensões funciona da maneira que já sabemos, ou seja, vai reduzindo até chegar a zero na , assim tem-se que:
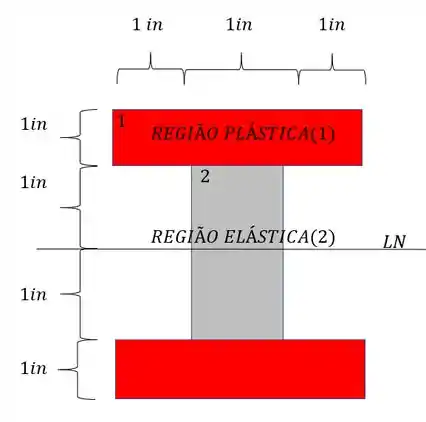
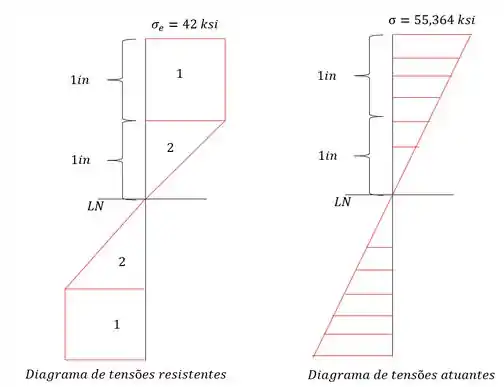
E o diagrama de tensões é dado por: (Vale lembrar que na região plástica máxima é a de escoamento, que fica constante até o ponto da região plástica)

Como temos seções acima e embaixo, temos que multiplicar por 2, assim, o nosso momento vai ser dado por:
Sabemos que a equação de tensão é dada por:
Agora pensa no seguinte, sabemos que o momento máximo que age na nossa seção é dado por:
O ponto que queremos saber o que ocorre é o dado por:
E o nosso momento de inércia vai ser dado por:
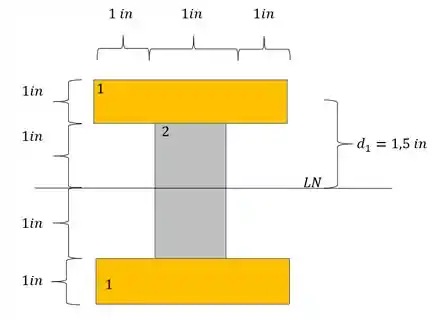
Assim temos que:
Substituindo na nossa equação teremos que:
Agora pensa no seguinte, o nosso diagrama de tensão máxima atuante na nossa seção é dado por:

E pensa no seguinte, qual a máxima tensão que a nossa estrutura suporta, se desenhássemos o diagrama, ela seria dada por:
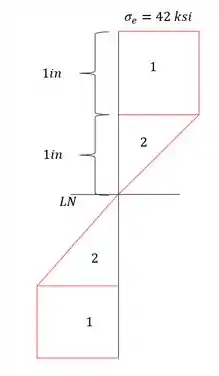
O seja, se fizermos um diagrama menos o outro temos o diagrama de tensões residuais em todos os pontos da viga, porém, pensa no seguinte, o item a) só pediu a tensão residual APENAS, no ponto , assim, temos que a tensão residual é dada por.
Passo 2
Para o item 2 temos que comparar os dois diagramas.
Agora pensa no seguinte, a tensão atuante começa em 55,364 e vai reduzindo até zero, certo? Como fazemos a tensão atuante menos a tensão resistente, quando a atuante chegar em , ela vai zerar a tensão residual, ou seja, só precisamos saber a altura em que a seção tem no diagrama de tensões atuante, assim teremos que:
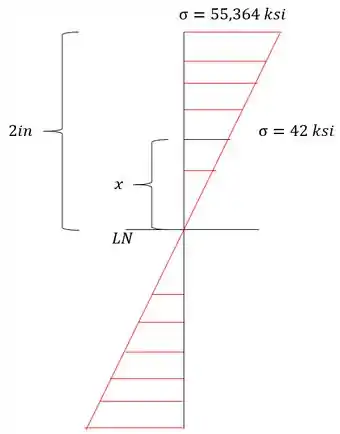
Ou seja, os pontos em que o diagrama de tensões residuais zera são os pontos:
Passo 3
Para lembrar como determinar o raio de curvatura, precisamos lembrar da seguinte relação:
Como queremos o raio de curvatura, podemos definir que:
Dessa equação, quem você conhece de cara é o valor do modulo de elasticidade, que pode ser concebido como:
E você pode estar se perguntando, qual tensão e qual y deve ser usado? A altura que deve ser usada é muito simples, é a altura que marca a passagem do estado plástico para o estado elástico, ou seja, no nosso caso, no nosso diagrama, isso ocorre na altura de e qual tensão usar? Não queremos o raio de curvatura baseado nas tensões residuais? Então precisamos da tensão residual, comparando os dois gráficos teremos que:
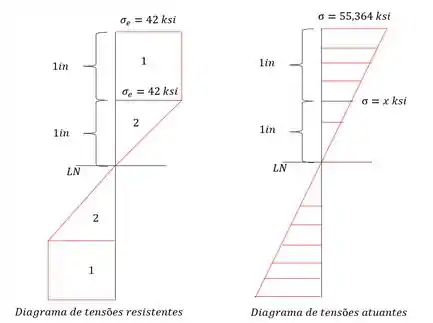
Obtendo a tensão atuante temos que:
Assim a tensão residual nesse ponto vai ser dado por:
Substituindo tudo na nossa fórmula vamos ter que: