Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 78b
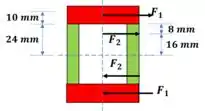
Uma viga de seção transversal mostrada é feita de um aço que é considerado ser elastoplásticos, com E=200GPa e . Por flexão em torno do eixo , determinar o momento fletor e o raio de curvatura, para que: (a) ocorra o início do escoamento; (b) as zonas plásticas, superior e inferior, da viga tenham 20 mm de espessura.
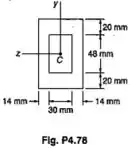
Passo 1
Vamos seguir o conselho de Einstein. Vamos fazer um desenho e destacar em vermelho a região plástica.
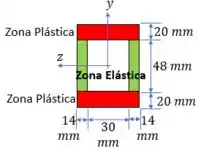
Assim fica fácil de ver que a espessura da zona elástica é:
Então metade da espessura é:
Passo 2
Como agora estamos trabalhando em regime elastoplásticos, a gente pode calcular o raio de curvatura utilizando a equação:
Passo 3
Para calcular o momento aplicado vamos voltar pra teoria das tensões. Observe a figura abaixo, na região plástica a tensão é constante, já na região elástica a tensão é linear.
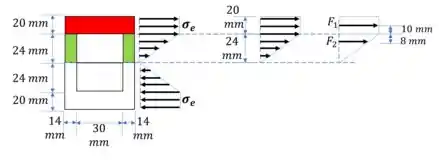
Vamos lembrar que a tensão é dada por . Com isso em mente, podemos calcular duas forças equivalentes às tensões.
A primeira parte da tensão tem formato retangular, então:
A segunda parte da distribuição de tensão tem formato triangular, logo:
Como a viga é simétrica, as regiões superior e inferior sofrem os mesmos esforços, porém, em compressão! Essas forças formam binários, e a resultante destes binários é o momento sobre a viga.
