Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 146
A viga I suporta a força de 1000 lb e o par de 2000 lb-ft aplicado ao suporte de 2 pés soldado na extremidade da viga. Calcule o cisalhamento V e o momento M na seção intermediária entre A e B.
Passo 1
Observe que podemos determinar a força de cisalhamento e o momento no ponto necessário cortando-o e analisando a peça à esquerda, incluindo o ponto A. Obviamente, precisaremos determinar a força de reação em A antes de podermos determinar a força de cisalhamento e o momento em necessário ponto médio.
Desenhe o diagrama de corpo livre da viga.
Passo 2
Ao igualar a soma dos momentos sobre o ponto B a zero, podemos determinar a força YA
A seguir, cortaremos o ponto C e analisaremos a parte da viga à esquerda.
Passo 3
Observe que as forças internas e o momento atuando na viga (VC e MC) são assumidos como tendo direção positiva, ou seja, sentido positivo.
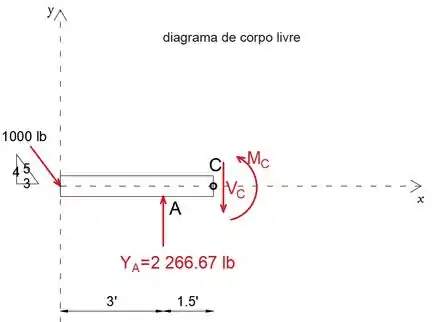
Ao igualar a soma das forças na direção y a zero, podemos determinar a força interna VC
Passo 4
Ao igualar a soma dos momentos sobre o ponto C a zero, podemos determinar o momento interno em C