Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 88
Determine a área total da superfície do corpo gerada girando a área sombreada em 36 ∘ em torno do eixo x.
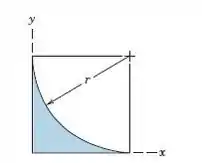
Passo 1
Usando o teorema de Pappus, podemos escrever a expressão para a área do corpo como
Onde x ‾ é o centróide da linha de um quarto do círculo, L é o comprimento da linha e o ângulo de rotação θ
Podemos ver no esboço as seguintes dimensões:
A expressão acima também pode ser escrita como:
Enquanto o comprimento da linha é igual a um quarto do comprimento do círculo completo.
E o ângulo de rotação
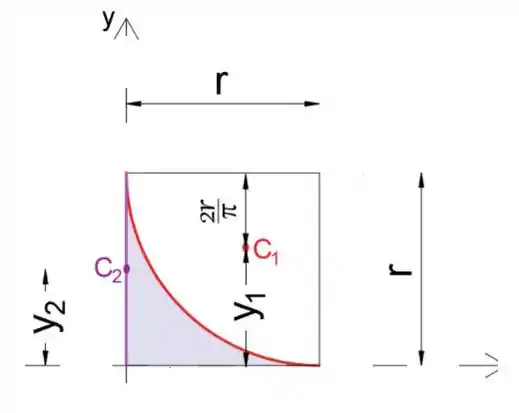
Passo 2
Coloque os valores na expressão (1)
Área total da superfície
Resposta
Exercícios de Livros Relacionados
Localize o centroide y da seção transversal da viga montada a partir de uma canaleta e de uma placa. Suponha que todos os cantos sejam “vivos” e desconsidere o tamanho da solda em A.
Determine a localização y do eixo x–x que passa pelo centroide da área transversal da viga. Para o cálculo, desconsidere o tamanho das soldas nos cantos em A e B.
Uma estante é feita de chapa de aço laminado e possui a seção transversal mostrada na figura .Determine a localização (x, y) do centroide da seção transversal. As dimensões são indicadas para cada seg
Localize o centroide (x, y) da seção transversal do elemento.
Determine a localização (x, y, z) do centroide do elemento homogêneo.