Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 47
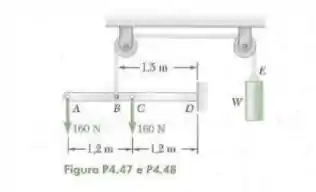
47. A viga sustenta duas cargas de mostradas na figura. A viga é mantida em posição por um engaste em e por um cabo que está preso ao contrapeso . Determine a reação em quando , .
Passo 1
Primeiramente, para determinar o que o enunciado quer, temos que quais são as possíveis reações que podem ocorrer em .
Nessa situação temos um engaste e segundo a figura do livro temos três reações possíveis, um momento em relação ao ponto , uma força que a parede faz no membro na direção e uma força na direção .
Então para achar o que o enunciado quer, vamos usar as equações de equilíbrio referente a força e ao momento ao nosso favor.
Para o cálculo do momento vamos considerar o sentido anti-horário como o sentido positivo.
A forma que iremos resolver é a mesma tanto para o item quanto o que vai mudar será o valor de .
Passo 2
Vamos começar então com o item
Primeiro vamos a analisar a equação referente a força na direção , então:
Agora vamos analisar para direção .
Agora só falta calcular em relação ao momento, vamos lá então:
Passo 3
Vamos começar então com o item
Primeiro vamos a analisar a equação referente a força na direção , então:
Agora vamos analisar para direção .
Agora só falta calcular em relação ao momento, vamos lá então: