Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 107
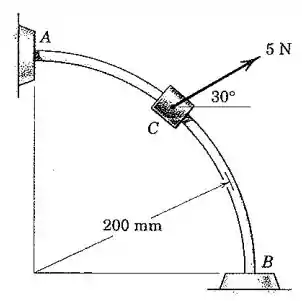
O cursor de parte do repouso em e desliza com atrito desprezível sobre a haste fixa no plano vertical. Determine a velocidade com que o cursor golpeia a extremidade quando atuado por uma força de , que possui uma direção constante. Despreze as pequenas dimensões do cursor.
Passo 1
Observe que de até , a força peso fará o seguinte trabalho sobre o cursor:
Já a componente vertical da força fará este trabalho:
Por fim, o trabalho da componente horizontal de será:
Passo 2
Como a variação da energia cinética de um corpo é igual ao trabalho total realizado sobre ele, temos:
Resposta
Exercícios de Livros Relacionados
3/134) O sistema é liberado a partir do repouso na posição mostrada . O cilindro de 15k g cai através do orifício no suporte , mas o disco de 15k g ( mostrado em corte) é removido do cilindro quando e
3/121) Um carro com uma massa de 1500k g parte do repouso na base de uma inclinação de 10 % e adquire uma velocidade de 50k m / h em uma distância de 100m com aceleração constante para cima na inclina
3/122) A resistência R à penetração x de um projétil de 0,25k g disparado com uma velocidade de 600m / s em um bloco de material fibroso é apresentada no gráfico . Represente essa resistência pela lin
3/129) O pequeno cursor de massa m é liberado a partir do repouso quando na posição A e então desliza ao longo da pista no plano vertical. A pista Elisa de A até D e rugosa .(coeficiente de atrito din
3/139) A força P = 40N é aplicada ao sistema , que está inicialmente em repouso . Determine as velocidades de A e B após A ter se deslocado 0,4m .