Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 125

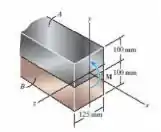
A viga composta é feita de aço A-36 (A) e latão vermelho C83400 (B) e tem a seção transversal mostrada na figura. Se for submetida a um momento M = 6,5 kN.m, determine a tensão máxima no latão e no aço. Determine também a tensão em cada material na junção entre eles.

Passo 1

Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questão de hoje nos traz uma viga composta por dois materiais diferentes, mas vou te explicar direitinho. Os materiais que compõem são o aço e o latão, e ele nos pede para calcular as duas tensões de flexão máximas (tanto para o aço quanto para o latão) e pegaremos o menor (afinal, se pegarmos o maior, o ‘’mais fraco’’ vai se romper com o momento do outro) para um momento fletor igual a 6,5 kN.m. Viu?? Ela só tem cara de malvada, mas vamos resolver rapidinho. Vem comigo!!

Passo 2

A primeira coisa que precisamos achar é a relação entre os coeficientes Elat e Eaço e o novo comprimento da viga.

Temos por teoria que o modulo de elasticidade do Latão é de 101 G P a , e o do aço e de 200   G P a

Substituindo teremos:

n   =     E l a t   E a ç o  

n = 101 200 = 0.505

b’ = nb = 0,505 x 125 = 63,125 mm

Agora que sabemos o comprimento e a altura de cada um dos nossos elementos da viga, vamos descobrir nosso ycc

y c c   =   ∑ A y c c ∑ A =   63,125 x 100 50 + 2 125 x 100 63,125 x 100 + ( 100 x 125 )

y c c = 116,4452   m m

Passo 3

Agora que já temos nossas dimensões, podemos calcular o momento máximo da viga. Para isso, vamos calcular primeiro o nosso I, para só depois substituir na nossa formulinha.

I   = 0,063125 0,1 3 12 + 0,063125 x 0,1 x ( 0,1164452 - 0,05 ) ² + 0,125 0,1 3 12 + 0,125 x 0,1 x ( 0,150 - 0,1164452 ) 2

I   =   5,76206   x   10 - 5   m 4

σ a ç o - m =   M   c I = 6500 x 0,0835548 5,76206   x   10 - 5   = 9,42   M P a

σ l a t - m =   n M   c I = 6500 x 0,0835548 x 0,505 5,76206   x   10 - 5   = 6,63   M P a

Na junção, teremos:

σ a ç o - j =   M   c I = 6500 x 0,0164452 5,76206   x   10 - 5   = 1,82   M P a

σ l a t - j =   n M   c I = 6500 x 0,0164452 x 0,505 5,76206   x   10 - 5   = 0,937   M P a

Resposta

σ a ç o - m =   9,42   M P a              

σ l a t - m = 6,63   M P a              

σ a ç o - m =   1,82   M P a              

σ l a t - m = 0,937   M P a              

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de concreto armado é feita com duas hastes de reforço de aço. Se a tensão de tração admissível para o aço for (σaço)adm = 280 MPa e a tensão de compressão admissível apara o concreto for (σconc
Determine o maior valor das forças aplicadas P se a tensão de flexão admissível for (σadm)c = 50 MPa sob compressão e (σadm)t = 120 MPa sob tração.
A braçadeira circular de mola produz uma força de compressão de 3 N sobre as chapas. Determine a tensão de flexão máxima produzida na mola A. A mola tem seção transversal retangular, como mostra a fig
Determine a força de compressão máxima que a braçadeira de mola pode exercer sobre as chapas se a tensão de flexão admissível para a braçadeira for σadm = 4 MPa.
Para a cantoneira e o carregamento do Problema Resolvido 6,6 verifique se ∫ q dz =0 ao longo da aba horizontal da cantoneira d ∫ qd y = P ao de sua aba vertical.