Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 13

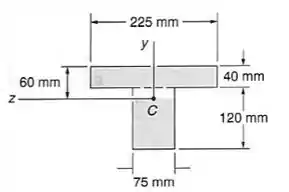
Sabendo-se que uma viga de seção transversal, como mostrado, é encurvado em torno de um eixo horizontal e está submetido a um momento fletor de 5,7   k N m , determinar a intensidade total da força atuando:

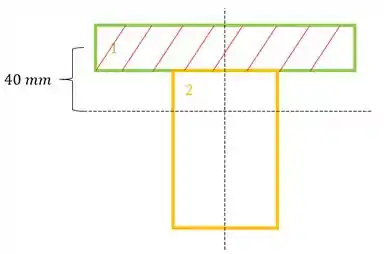
  1. Na aba superior
  2. Na porção sombreada da alma.

Passo 1

Sabemos que queremos determinar as forças que agem nas abas sombreadas da nossa estrutura, para isso sabemos que a tensão devido a um momento fletor é calculado com a seguinte equação.

σ x = - M y I

Se quisermos determinar a força com relação a tensão, podemos usar a seguinte equação.

d F = σ x   d A = - M y I   d A

Integrando teremos que:

F = ∫ d F = - ∫ M y I   d A = - M I ∫ y   d A = - M I y * A *

Em que:

y * = d i s t â n c i a   d o   c e n t r o i d e   d a   á r e a   a   s e r   c a l c u l a d a   a   f o r ç a   a t é   a   L N

A * = Á r e a   q u e   v a i   s e r   c a l c u l a d a   a   f o r ç a

Agora só precisamos determinar as opções, vamos primeiro determinar os itens que são comuns aos dois.

Passo 2

  • M

    • O momento fletor é tranquilo, podemos usar o que foi dado no enunciado, sendo assim teremos que:

    M = 5,7   k N m = 5700   k N m m

    E também temos as medidas.

  • I

    Para o cálculo do momento de inércia precisamos seguir um passo a passo dado da seguinte maneira:

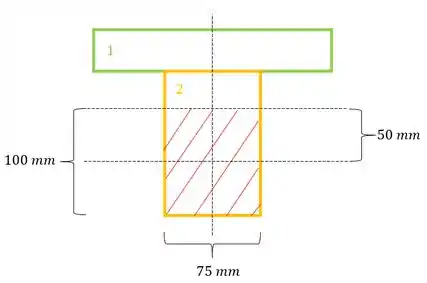
    • Numeração das regiões

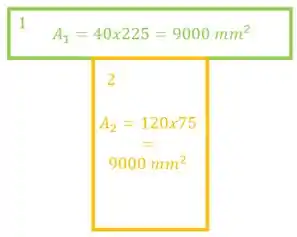
    • Área das regiões

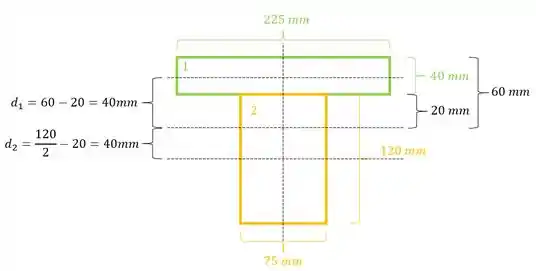
    • Distância do centroide das áreas até a LN

    • Momento de inércia de cada região

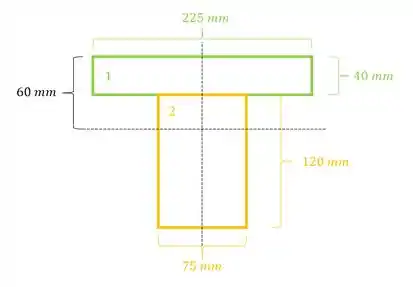
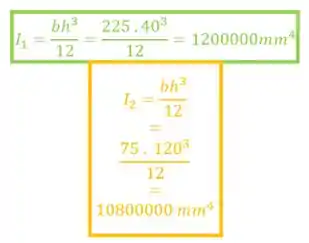
    • Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:

    I = ∑ I i + A i d i 2

    Sendo assim teremos que:

    I = I 1 + A 1 d 1 2 + I 2 + A 2 d 2 2

    I = 1200000 + 9000   .     40 2 + 10800000 + 90000   .     40 2 = 40800000   m m 4

    Passo 3

    E agora precisamos definir os valores das áreas em que queremos saber a força que está agindo, sendo assim teremos que:

  1. Vamos definir:
  2. y *

  3. A *

  4. F

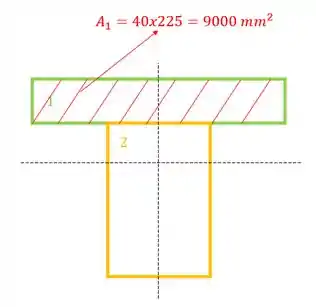
    5. Calculando a força teremos que:

    F = - M I y * A *

    F = - 5700   k N m m 40800000   m m 4 40   m m   .   9000   m m 2 = - 50,3   k N

  5. Vamos definir:
  • y *

  • A *

  • F

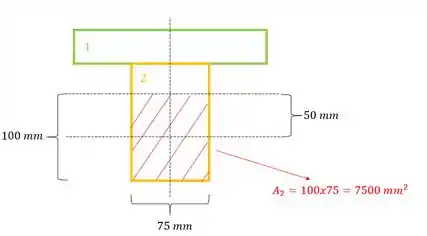
    • Calculando a força temos que lembrar que como o Y dessa vez está para baixo, ele será negativo, sendo assim teremos que:

    F = - M I y * A *

    F = - 5700   k N m m 40800000   m m 4 - 50 m m   .   7500   m m 2 = 52,4   k N

    Resposta

    1. F = - 50,3   k N
    2. F = 52,4   k N
    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Sabendo que a viga A B está em equilíbrio sob o carregamento mostrado, trace os diagramas de força cortante e momento fletor para essa viga e determine a tensão normal máxima provocada pelo momento fl
    A viga A B suporta uma força uniformemente distribuída de 2k N / m e duas forças concentradas P e Q . Foi determinado experimentalmente que a tensão normal provocada pelo momento fletor na borda infer
    Sabendo que a tensão admissível para ao aço é de 160M P a , selecione a viga de mesa larga mais econômica para suportar o carregamento mostrado.
    Trace os diagramas de cortante e momento fletor para a viga e o carregamento mostrado, e determine a tensão normal máxima provocada pelo momento fletor.
    Para a viga e o carregamento mostrados na figura, projete a seção transversal da viga sabendo que o tipo de madeira utilizada tem uma tensão normal admissível de 12M P a .