Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 78

Se a viga tiver seção transversal retangular com largura de 200   m m e altura 400   m m , determine a tensão de flexão máxima absoluta na viga.

Passo 1

Precisamos do diagrama de momento para determinar o momento máximo. Para isso, precisamos do momento no engaste:

∑ M a = 0 → M = 200 + 40 × 3,6 + 50 × 2,4 + 30 × 2,4 × 1,2 = 0

M = 550,4 k N m

Logo, podemos fazer o diagrama:

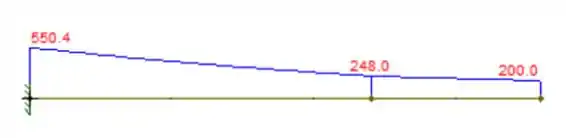
Passo 2

Podemos agora calcular a tensão máxima:

σ m a x = 550,4 × 10 3 , 2 0,2 × 0,4 3 12 = 103,2 M P a

Resposta

σ m a x = 103,2 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de aço mostrada é feita de um aço com σe=250 MPa e σu=400 MPa. Usando um coeficiente de segurança de 2,5, determinar o maior momento que pode ser aplicado à viga, quando ela se encurva em torno
A viga de aço mostrada é feita de um aço com σe=250 MPa e σu=400 MPa. Usando um coeficiente de segurança de 2,5, determinar o maior momento que pode ser aplicado à viga, quando ela se encurva em torno
A viga de seção transversal, como indicado, é extrudada de uma liga de alumínio com σe = 310 MPa e σu = 480 MPa. Usando um coeficiente de segurança 3,0, determinar o maior momento que pode ser aplicad
Sabendo-se que o momento mostrado atua no plano vertical, determinar a tensão nos pontos A e B.
Duas forças verticais são aplicadas a uma viga de seção transversal mostrada. Determinar as máximas tensões de tração e compressão na porção BC da viga, sabendo que a nova largura da aba é de 130 mm.