Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 132
Um torque é aplicado ao eixo que tem raio de 100mm. Se o material obedecer a uma relação de tensão-deformação por cisalhamento de , determine o torque que deve ser aplicado ao eixo de modo que a máxima deformação por cisalhamento se torne 0,005 rad.
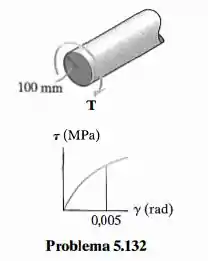
Passo 1
Dados da questão:
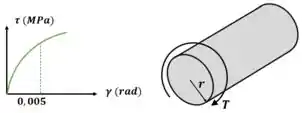
O que a questão pede:
- O torque para atingir a deformação de 0,005 rad.
Estratégia de resolução: O torque é definido pela equação integral 5.23. Mas ela é integrada em relação ao raio. Então primeiro precisaremos relacionar o raio com a deformação, para depois aplicar a equação 5.23
Passo 2
A proporção entre deformação e o raio é constante ao longo de uma seção transversal:
A questão nos diz que a deformação máxima é , sabemos que a deformação máxima ocorre na parte mais externa do eixo :
Observe que usamos o raio em metros. Precisaremos manter isso ao longo de todo o exercício.
Passo 3
Agora podemos aplicar a equação 5.23
Substituindo a fórmula da tensão
Substituindo a fórmula da deformação
Substituindo o valor do raio
Como utilizamos a tensão em MPa e o raio em metros, encontramos um torque em meganewtons vezes metro
Convertendo: