Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 2
2. A coluna é composta por um elemento estrutural rígido preso por um pino na base e acoplado a uma mola no topo. Se a mola não estiver esticada quando a coluna estiver em posição vertical, determine a carga crítica que pode ser aplicada à coluna.
Passo 1
Vamos inicialmente, fazer um esboço das forças agindo no nosso sistema, na hipótese de que ele está inclinado de um ângulo com a vertical, devido a ação da força .
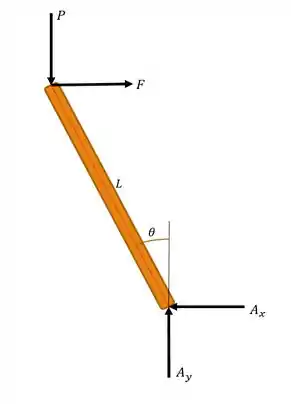
Passo 2
Agora, façamos o somatório das forças e momentos em relação a um ponto conveniente na nossa figura. Pode ser o ponto ! Que tal!
Aplicando o somatório das forças no ponto , numa situação em que a barra está em estado iminente de flambagem, temos que:
Só que na verdade é a força elática igual a . E esse da fórmula, se for olhar a figura do , dá pra ver claramente que ele é igual . Logo, ficamos com:
Mas olha só que coisa boa! Sabemos que a mola não está esticada quando a coluna estiver em posição vertical. Ou seja, o nosso ângulo vale zero. E qual é mesmo o cosseno de ? Isso mesmo,. Assim, chegamos à seguinte relação:
Ora bolas! Se a nossa força está concentrada em uma das extremidades da coluna, no chamado ponto de bifurcação, precisa perder tempo tentando encontrar a carga crítica de flambagem, . A carga crítica, obviamente, vai ser igual a .