Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 104

A viga uniforme de está apoiada pela corda que está à ponta da viga, passa pelo pino rugoso e depois é conectada ao bloco de . Se o coeficiente de atrito estático entre a viga e o bloco e entre a corda e o pino é , determine a distância máxima em que o bloco pode ser colocado a partir de e ainda permanece em equilíbrio. Assuma que o bloco não tombará.

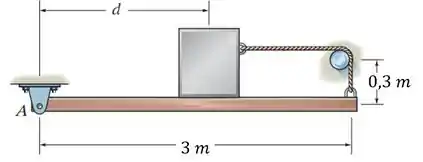
Passo 1

Primeiro vamos marcar as forças na ilustração, se liga só:

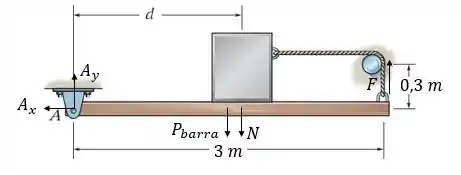
Passo 2

Como nosso bloco está em equilíbrio, temos:

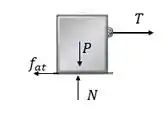
Para o eixo :

Então,

Paara o eixo :

Assim,

Como :

Agora vamos olhar para roldana. Usando aquela formula da teoria:

Como e :

Fazendo as contas:

Passo 3

Pra finalizar vamos fazer torque com relação ao ponto A, pois não sabemos a força nesse ponto. Considerando positivo no sentido anti-horário:

Substituindo os valores:

Fazendo as contas:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a relação de atrito entre as trações na correia, o coeficiente de atrito m e os contatos angulares α e β para a correia em “ V ” é T 2 = T 1 e μ β / sen ⁡ ( α / 2 ) .

Um cabo é preso à placa B de 20k g , passa por um pino fixo em C e é preso ao bloco em A .Usando os coeficientes de atrito estático mostrados, determine a menor massa do bloco A que impeça o movimento

Determine a força P que deverá ser aplicada ao cabo da alavanca para que a roda esteja na iminência de girar se M = 300N ⋅ m . O coeficiente de atrito estático entre a correia e a roda é μ s = 0,3 .

A corda suportando o cilindro de 6k g passa por três pinos, A ,B ,C , onde μ s = 0,2 . Determine a faixa de valores para a intensidade da força horizontal P para a qual o cilindro não subirá nem desce

Determine a menor força P necessária para levantar a caixa de 40k g . O coeficiente de atrito estático entre o cabo e cada pino é μ s = 0,1 .