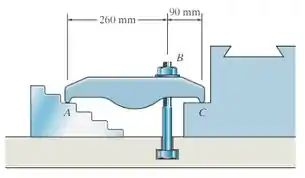
A peça da máquina é mantida no local usando o grampo com dupla extremidade. O parafuso em tem roscas quadradas com um raio médio de e um passo de e o coeficiente de atrito estático com a porca é . Se um torque de é aplicado à porca para apertá-la, determine a força normal do grampo nos contatos lisos e .
Passo 1
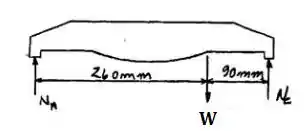
Um bom início de questão para mecânica é sempre que possível (na maior parte das vezes vai ser) desenhar o diagrama de corpo livre do objeto em questão. Isso vai nos ajudar e muito a entender o que se passa na questão e o que queremos encontrar!
Passo 2
Galera, para um parafuso de rosca quadrada, o ângulo de passo é determinado a partir de . Aqui, é o passo da rosca e é o raio médio da rosca. Tendo essa ideia em mente, vamos calcular o ângulo de passo da nossa questão:
Passo 3
O ângulo de atrito estático para o parafuso de rosca quadrada é dado por . Logo,
Passo 4
A equação para o momento do parafuso é dada por:
Substituindo os valores na equação, temos:
Passo 5
Vamos calcualr agora os valores das reações de apoio em e . O somatório de momentos num sistema em quilíbrio é igual a zero. Assim, vamos calcular o momento em relação ao ponto para encontrarmos o valor de . Assumindo que o sentido anti-horário é positivo, temos:
Para encontrarmos o valor de podemos analisar o somatório das forças verticais desse sistema. Sabemos que, em todos sistema em equilíbrio, o somatório das forças verticais é igual a erro. Assim, adotando como referencial positivo para cima, temos:
Resposta
As forças de contato em são iguais a: