Para a viga uniforme em balanço e o carregamento mostrados nas figuras, determine (a) a inclinação e (b) a deflexão na extremidade livre.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o método do momento de área. Para isso vamos precisar desenhar o diagrama M/EI para a viga. Depois disso, sabemos que a área entre dois pontos sob a curva M/EI representa a inclinação entre esses dois pontos. E para obter a deflexão, vamos utilizar o teorema do segundo momento de área, que nos fornece o desvio tangencial entre dois pontos. Sabendo disso, temos tudo o que precisamos para resolver o exercício, então bora lá!
Passo 2
Beleza! No nosso caso, como temos somente a força P localizada na extremidade livre da viga, ela irá causar um momento de grandeza:
Conforme vai se afastando do ponto A e chegando em B, até o momento máximo . Então o nosso diagrama será uma linha inclinada, aumentando gradativamente de A até B, da seguinte forma:
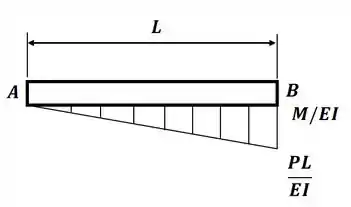
Então, para a letra (a), temos que a inclinação na extremidade livre, será a inclinação entre os pontos A e B, que nada mais é do que a área abaixo da curva , ou seja:
Como temos um engaste no ponto B, não teremos inclinação nesse ponto. E, através do diagrama, é fácil ver a área abaixo da curva, então nossa equação acima se torna:
Beleeeza! Bora pra (b) agora.
Passo 3
Agora, para a letra (b), sabemos que a deflexão na extremidade livre será dada através do teorema do segundo momento de área, que é dado por:
Em que é a área embaixo da curva e é a distância do centroide da área até o eixo vertical que passa pelo ponto de interesse, que no nosso caso é o ponto A. Então, como temos uma área embaixo da curva com formato triangular, nossa deflexão em A será:
Shoow! Terminamos mais um, valeeu!