Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 134

Para a viga uniforme com o carregamento mostrado, determinar a reação em cada um dos apoios.

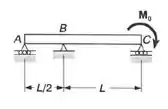
Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

Remova o suporte C e trate R c como redundante.

Considere as cargas M o e R c separadamente.

Coloque a tangente de referência em A.

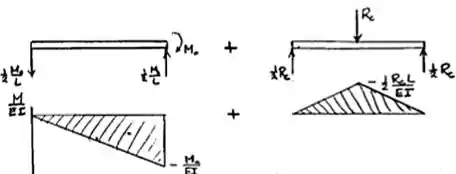
t B / A = - 1 2 M o E I 2 L 2 L 3 + 1 2 1 2 R c L E I 2 L L = - 2 3 M o L 2 E I + 1 2 R c L 3 E I

Passo 2

t C / A = - 1 2 1 2 M o E I L L 3 + 1 2 1 2 R c L E I L L 3 = - 1 12 M o L 2 E I + 1 12 R c L 3 E I

y c = t C / A - X C / A X B / A     t B / A = t C / A - 1 2 t B / A = 0

- 1 12 + 1 3 M o L 2 E I + 1 12 - 1 4 R c L 3 E I = 0

R C = 3 2 M o L ↓  

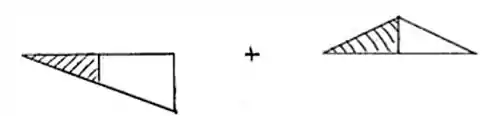
Passo 3

Consideramos

R A = 1 2   R C - 1 2 M o L = 1 4 M o L ↑

R B = 1 2   R C - 1 2 M o L = 5 4 M o L ↑

Resposta

R A = 1 4 M o L ↑

R B = 5 4 M o L ↑

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a reação no apoio móvel e trace o diagrama de momento fletor para a estrutura.
Três hastes, cada uma com a mesma rigidez E I , são soldadas para formar o pórtico. Para o carregamento mostrado, determine a deflexão no ponto D .
Duas barras A B e B C de mesma rigidez à flexão E I são soldadas juntas em B . Para o carregamento mostrado, determine (a) a deflexão do ponto C e (b) a inclinação do elemento B C no ponto C .
Três barras do mesmo material e mesma área são usadas para suportar a força P . Determine o esforço na barra B C .
Determine a reação no apoio móvel e trace o diagrama de momento fletor para a estrutura.