Fórmula da Torção
Teoria
Introdução
Vamos dizer que a gente quer estudar o eixo abaixo, que tem um raio e duas hastes laterais no ponto :
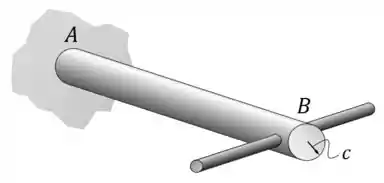
Um dos jeitos que a gente pode carregar esse eixo é aplicando uma carga axial nele:
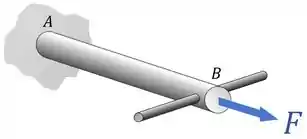
Nesse caso, sabemos que:
- Essa força axial vai gerar ao longo do eixo uma força interna normal ;
- E que essa força interna normal vai gerar uma tensão normal no eixo.
Agora, outra forma que a gente pode carregar esse eixo é aplicando um torque nele, como na imagem abaixo:
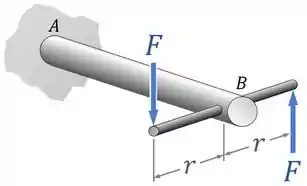
Olha só...
Fazendo o somatório de forças na vertical, essas duas forças vão se cancelar.
Mas isso não impede cada uma dessas duas forças de gerar no eixo principal um torque .
Dessa forma, vamos ter um torque resultante no ponto do eixo:
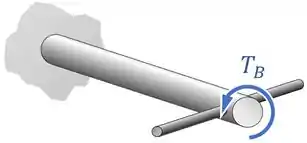
Aí aqui surge uma dúvida... 😯
Se um carregamento axial gera uma força interna normal e uma tensão normal numa peça, o que é que esse torque vai gerar no nosso eixo?
Como é a tensão gerada por esse torque?
Torque Interno
Bom...
Acabamos de revisar um pouco acima que a primeira coisa que uma força axial gera em um eixo é uma força interna ao longo de todo o eixo.
Então a primeira coisa que o nosso torque externo vai gerar no nosso eixo vai ser um torque interno ao longo de todo o eixo.
Ou seja, se olharmos para uma seção transversal qualquer do nosso eixo, vamos encontrar esse torque interno :
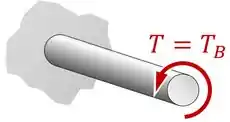
Beleza...
E o que é que esse torque interno vai causar na nossa peça?
Deformação devido ao Torque
Para responder isso, vamos ter que desenhar uma linha reta passando pela nossa peça e por uma seção transversal dela:
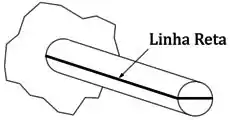
À medida que a nossa peça for carregada com o torque externo e tiver que resistir ao torque interno gerado nela, essa linha reta vai se deformar assim:
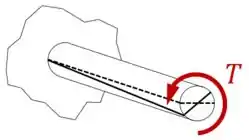
E isso nos mostra que, na seção transversal do eixo:
- O centro do eixo não sofre nenhuma deformação;
- Os pontos mais externos do eixo, distantes do centro pelo raio , vão sofrer uma deformação máxima;
- E qualquer outro ponto, distante do centro por um raio (), vai sofrer uma deformação que cresce linearmente com o aumento de ,
Como mostra a imagem abaixo:
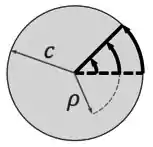
Agora, pensa aí...
Essa deformação que estamos vendo ocorre nas faces das seções transversais do nosso eixo.
E a gente sabe que tensão e deformação normal são aquelas que ocorrem na direção normal das seções transversais de uma peça.
O que acontece nas faces das seções transversais, é tensão (e deformação) cisalhante.
Então daqui, já conseguimos concluir que a tensão que um torque gera em um eixo é uma tensão cisalhante, representada pela letra grega (“tau”).
Distribuição de Tensão
Em seguida, podemos pensar o seguinte:
Se a deformação na seção transversal do nosso eixo cresce linearmente à medida que a gente se afasta do centro, o mesmo deve acontecer para a tensão.
E na prática, é isso mesmo que acontece.
Então se a gente for visualizar a distribuição de tensão cisalhante ao longo de uma linha qualquer em uma seção transversal do nosso eixo, vamos ver a distribuição triangular abaixo:
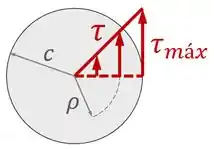
Onde a distribuição de tensão varia de em até em .
E caso o nosso eixo fosse vazado com um raio interno , a distribuição continuaria com esse aspecto triangular, mas variaria de em até em :
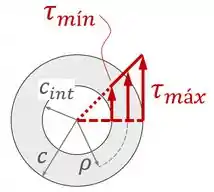
Ok! 👍
E se a gente precisar calcular a tensão em um ponto do nosso eixo ou até a tensão máxima nele?
Fórmula da Torção
Para isso, existe a fórmula da torção:
Onde:
1. é o torque interno no eixo, também conhecido por alguns livros como o Momento Torsor ;
2. é a distância do ponto que está sendo estudado ao centro do eixo;
& 3. é o “momento polar de inércia” da seção transversal do eixo, que é dado pelas fórmulas:
Muitas vezes, só queremos saber a tensão cisalhante máxima em um eixo, então usamos um caso específico da fórmula da torção em que para encontrar que:
E algumas vezes, vamos querer calcular a tensão mínima em um eixo vazado. Nesses casos, basta aplicar para encontrar que:
Resumo
Para facilitar sua vida, segue um resumo do que você precisa saber para resolver exercícios envolvendo a fórmula da torção:
Pronto!
Agora se você quiser treinar, é só seguir para os exercícios que nós separamos e resolvemos alguns pensando nisso.
Torque Interno
Deformação devido ao Torque
Distribuição de Tensão
Fórmula da Torção
Resumo
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 134-5.1.
Um eixo é feito de aço com tensão de cisalhamento admissível . Se o diâmetro do eixo for , determine o torque máximo que pode ser transmitido. Qual seria o torque máximo se fosse feito um furo de de diâmetro no eixo? Faça um rascunho da distribuição da tensão de cisalhamento ao longo de uma linha radial em cada caso.
Passo 1
O que está acontecendo?
O exercício quer que a gente estude dois eixos com um diâmetro de : um maciço e um vazado, com um diâmetro interno de .
Sendo assim, esses eixos vão ter:
Um raio externo ;
E um raio interno , no caso do eixo vazado.
E o que é que o exercício quer?
Ele quer saber qual são os torques máximos e que podem ser transmitidos pelos eixos maciço e vazado, respectivamente.
Esses torques máximos vão ser os torques que vão gerar, de acordo com a fórmula da torção...
...uma tensão de cisalhamento nos eixos igual à tensão de cisalhamento admissível .
Dessa forma, podemos aplicar as condições...
...e desenvolver essas expressões para encontrar os torques máximos e .
Além disso, o exercício ainda quer que a gente esboce a distribuição da tensão de cisalhamento ao longo de uma linha radial em cada eixo.
Passo 2
Vamos começar pelo cálculo do torque máximo no eixo maciço.
Começamos aplicando a condição:
E substituindo a fórmula da torção:
Em seguida, isolamos para encontrar que:
Agora, para calcular o torque máximo , vamos ter que conhecer o momento de inércia polar da seção transversal do nosso eixo.
Então lembra aí!
Para um eixo maciço de raio , a fórmula desse momento de inércia polar é:
Com isso, o nosso torque máximo fica assim:
Simplificando tudo, encontramos que:
Finalmente, substituindo:
;
& ,
temos que:
O que dá:
Como esse resultado é muito grande, podemos reescrevê-lo em :
Passo 3
Em seguida, vamos fazer o cálculo do torque máximo no eixo vazado.
Mais uma vez, começamos aplicando a condição:
E substituindo a fórmula da torção:
Isolando , encontramos que:
E... Lembra aí!
O momento de inércia polar de um eixo vazado de raio externo e raio interno é dado pela fórmula:
Dessa forma, o nosso torque máximo fica assim:
E, simplificando tudo, isso fica assim:
Finalmente, substituindo:
;
;
& ,
encontramos que:
Como esse resultado é muito grande, podemos reescrevê-lo em :
Passo 4
Por fim, vamos esboçar as distribuições da tensão de cisalhamento ao longo de uma linha radial em cada eixo.
Então vamos nos lembrar do que vimos na teoria...
Essa distribuição é linear, variando desde no centro dos eixos até (que vai ser igual à nos nossos casos) na superfície externa dos eixos:
Agora, para completar esses esboços, só precisamos calcular qual é a tensão na superfície interna do eixo vazado.
Para isso, usamos a fórmula da torção em sua versão geral, que fornece a tensão em um ponto distante um raio do centro do eixo:
No nosso caso, queremos saber a tensão na superfície interna do eixo vazado, onde , e temos que .
Então essa fórmula fica assim:
Por fim, substituindo:
;
;
& ,
encontramos que:
Com isso, os nossos esboços ficam assim:
E assim terminamos o exercício!
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 135-5.10.
O elo funciona como parte do controle do elevador de um pequeno avião. Se o tubo de alumínio conectado tiver de diâmetro interno e parede de de espessura, determine a tensão de cisalhamento máxima no tubo quando a força de for aplicada aos cabos. Além disso, trace um rascunho da distribuição da tensão de cisalhamento na seção transversal.
Passo 1
O que está acontecendo?
As forças geram, com braços , um torque de sentido anti-horário () no tubo vazado de alumínio.
Esse tubo tem um diâmetro interno e uma espessura de .
Com isso, conseguimos concluir que:
1. O tubo tem um diâmetro externo , e, consequentemente, um raio externo :
& 2. O tubo tem um raio interno :
E o que é que o exercício quer saber?
Ele quer que a gente calcule a tensão de cisalhamento máxima no tubo quando as forças são aplicadas.
Para calcular essa tensão máxima, vamos usar a fórmula da torção:
Onde:
- é o torque resultante gerado pelas forças aplicadas;
- & é o momento de inércia polar do tubo vazado, que vai ser dado pela fórmula:
Além de tudo isso, o exercício também quer que a gente esboce a distribuição da tensão de cisalhamento na seção transversal do tubo.
Passo 2
Vamos começar pelo cálculo do torque resultante no tubo.
Esse torque vai ser o somatório dos torques causados por cada força .
E como essas forças possuem um braço , o torque causado por elas vai ser igual à .
Sendo assim, vamos ter que:
O que significa que:
Passo 3
Calculado o torque resultante no tubo, podemos seguir para o cálculo da tensão de cisalhamento máxima .
Para tanto, aplicamos a fórmula da torção:
Substituindo a expressão encontrada no Passo 2 para e a fórmula indicada no Passo 1 para , temos que:
E, arrumando tudo, isso fica assim:
Com isso, só falta substituir os valores:
- ;
- ;
- ;
- & ,
Para encontrarmos que:
Substituindo por e fornecendo o resultado final com três algarismos significativos, temos que:
Passo 4
Por último, para finalizar o exercício, vamos fazer o esboço da distribuição da tensão de cisalhamento na seção transversal do tubo.
Sabendo que essa distribuição varia linearmente:
- Desde no ponto central do tubo;
- Até na superfície externa do tubo,
Esse esboço fica assim:
Agora, esse esboço está incompleto porque a gente não sabe qual o valor da tensão na superfície interna do tubo vazado.
Para calcular a tensão em uma região de raio de um eixo, podemos usar a fórmula:
(Lembra? Essa fórmula pode ser obtida combinando as fórmulas e .)
Substituindo , e , conseguimos definir o valor da tensão na superfície interna:
Dessa forma, o nosso esboço final fica assim:
Resposta
Exercício Resolvido #3
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 165-3.7.
O sistema da figura é constituído por um eixo de seção transversal cheia e com uma tensão de cisalhamento admissível de , e por um tubo feito de latão com uma tensão de cisalhamento admissível de .
Determine o maior torque que pode ser aplicado em , sem que a tensão de cisalhamento admissível do material do tubo seja excedida e o valor correspondente necessário para o diâmetro do eixo .
Passo 1
O que está acontecendo?
O eixo maciço possui uma tensão de cisalhamento admissível e um raio , onde é o seu diâmetro.
Já o tubo tem:
- Uma tensão de cisalhamento admissível ;
- Um diâmetro externo de , e, consequentemente, um raio externo ;
- Uma espessura ;
- E um raio interno .
Eles estão submetidos a um torque .
E o que é que o exercício quer?
No item , ele quer saber o maior torque que pode ser aplicado sem que a tensão de cisalhamento do tubo seja excedida.
Ou seja, ele quer saber o maior torque que ainda gera, no tubo , uma tensão máxima que satisfaça a condição:
Então podemos usar essa condição e desenvolvê-la usando a fórmula da torção () para encontrar o torque máximo .
Já no item , ele quer saber o diâmetro necessário para o eixo para que ele suporte o torque encontrado no item anterior.
Para encontrar esse diâmetro, vamos aplicar a mesma condição que usamos com o tubo para o eixo :
Mas dessa vez, vamos desenvolver essa condição com o objetivo de encontrar o diâmetro mínimo.
Passo 2
Vamos começar resolvendo o item !
Para o tubo , temos que:
Aqui, a tensão máxima pode ser descrita pela fórmula da torção:
No caso do tubo , definimos o raio externo como .
Então a fórmula da torção aplicada para o tubo fica assim:
Substituindo isso na condição de projeto, temos que:
E isolando o torque aplicado , encontramos que:
Além disso, para o tubo , que possui um raio interno e um raio externo , o momento de inércia polar vai ser dado pela fórmula:
Dessa forma, a nossa expressão anterior fica assim:
Finalmente, substituindo os valores:
- ;
- ;
- & ,
Encontramos que:
Como esse número é muito grande, reescrevemos ele em :
Ou seja, o maior torque que pode ser aplicado em , sem que a tensão de cisalhamento admissível do material do tubo seja excedida, é:
Passo 3
Agora, resolvemos o item .
Para o eixo maciço , temos que:
Agora, aplicando a fórmula da torção para o eixo , temos que:
Dessa forma, a nossa condição anterior fica assim:
Aqui, temos que o momento polar de inércia do eixo maciço de raio vai ser dado pela fórmula:
Então podemos substituir isso na nossa expressão anterior para encontrar que:
Arrumando tudo, isso fica assim:
E, aqui, ainda podemos fazer mais uma substituição, que é a de que o raio do eixo é igual à metade do seu diâmetro .
Fazendo isso, temos que:
E, mais uma vez, arrumando tudo, temos:
Como queremos encontrar o diâmetro mínimo, devemos isolá-lo:
Espelhando essa expressão e fazendo a raiz cúbica, temos que:
Finalmente, substituindo:
- ;
- ,
Encontramos que:
Ou seja, o valor necessário para o diâmetro do eixo correspondente ao torque encontrado no item é:
E assim terminamos o exercício!
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 137-5.30.
O eixo maciço tem conicidade linear de em uma extremidade e na outra extremidade. Deduza uma equação que dê a tensão de cisalhamento máxima no eixo em uma localização ao longo da linha central do eixo.
Dica do Expert: Se o seu professor/a sua professora não for do tipo que cobra:
- Exercícios literais;
- Ou exercícios com peças com formatos alternativos (como a peça desse exercício),
Sinta-se livre para pular para os próximos tópicos, que têm exercícios mais prováveis de cair em prova. 😉
Passo 1
O que está acontecendo?
Em uma seção qualquer do eixo, a tensão de cisalhamento máxima vai ser dada pela fórmula da torção:
Sendo que, em todas as seções, o torque vai ser o mesmo e o raio das seções vai variar entre e , dependendo da posição da seção que estiver sendo estudada.
Além disso, como o eixo é maciço, o seu momento polar de inércia vai ser dado pela fórmula:
E o que é que o exercício quer?
Ele quer que a gente encontre a tensão de cisalhamento máxima no eixo em uma certa seção de posição .
Então primeiro, temos que descrever o raio de uma seção em função de sua posição .
Em seguida, vamos substituir o que encontrarmos nas fórmulas da torção e do momento polar de inércia .
Assim, vamos encontrar a tensão de cisalhamento máxima em uma seção de posição no eixo!
Passo 2
Então vamos começar descrevendo o raio de uma seção em função de sua posição .
Para fazer isso, precisamos fazer um desenho observando como o raio das seções varia entre e ao longo do comprimento do eixo do exercício:
Quase sempre que temos uma variável que varia linearmente, como é o caso do nosso raio , uma das formas de descrever essa variável é fazendo uma semelhança de triângulos.
Então vamos tentar isso!
Os triângulos que existem nesse desenho são os triângulos que podem ser formados acima do raio :
Aplicando a semelhança de triângulos entre:
- O triângulo menor, de base e altura ;
- E o triângulo maior, de base e altura ,
Temos que:
Passando os termos que estão dividindo para o outro lado, isso fica assim:
Em seguida, fazendo as distributivas, temos:
Cortando dos dois lados e colocando e em evidência, temos que:
Agora, como queremos definir o raio , devemos isolá-lo.
Fazendo isso, encontramos que:
Passo 3
Agora que já encontramos o raio de uma seção qualquer de posição , já podemos calcular a tensão de cisalhamento máxima nessa seção, que é o que o exercício quer!
Para tanto, aplicamos a fórmula da torção:
Substituímos a fórmula para o momento de inércia polar para um eixo maciço:
E simplificamos tudo, para encontrar que:
Agora, só falta substituir a expressão que encontramos para no passo anterior.
Fazendo isso, temos que:
Por fim, podemos deixar essa expressão mais bonita passando o para cima.
Fazendo isso, encontramos a nossa resposta final:
Resposta
Exercício Resolvido #5
Elaboração própria
Na figura baixo temos desenhado uma estrutura sujeita a dois carregamentos, uma carga de e um torque de . Considerando apenas os efeitos do esforço torsor, determine o valor do cisalhante máximo que ocorre no ponto A da nossa barra.
Passo 1
Podemos ver nessa questão que o nosso objetivo principal é determinar o valor do cisalhante máximo, antes de qualquer coisa devemos analisar, pelo enunciado, que devemos apenas considerar os efeitos do esforço torsor, logo só usaremos a fórmula
Porém também sabemos que queremos o cisalhante máximo, e para termos o cisalhante máximo devemos fazer pois para os efeitos do torsor os pontos mais extremos possuem os maiores cisalhantes.
Passo 2
Outra coisa que precisamos calcular é o nosso momento polar de inercia (). Aqui vale lembrar que o nosso momento polar de inercia é sempre da seção. Como no enunciado nos é dito que se trata de uma seção circular, usaremos como momento polar de inercia a equação
Substituindo na nossa equação principal, teremos que
Passo 3
O raio definimos facilmente, porém devemos tomar cuidado com o torsor, pois esse se trata do torsor máximo que está agindo na nossa peça, para descobrirmos o seu valor faremos a seguinte sequência de passos.
Primeiro cortamos a nossa barra no ponto que desejamos calcular o torsor
Em seguida levamos até essa seção todos os esforços que tínhamos antes de cortar e que após o corte não estamos vendo mais. Como só nos interessa analisar efeitos do torsor, podemos levar o nosso torque de diretamente para seção.
Também temos que levar os esforços torsores causados pela carga de . Para calcular o seu valor precisamos analisar o seu braço de alavanca, olhando a figura abaixo teremos que
Trocando a nossa carga pelo efeito torsor causado por ela teremos que
Levando esse esforço para nossa seção A teremos que
Logo também já temos o nosso torsor que age na peça que é dado por
Passo 4
Agora que já temos tudo que precisamos, basta substituir e determinar o valor do nosso cisalhante máximo
Substituindo teremos que
Resposta
Exercício Resolvido #6
Elaboração própria
Na figura baixo temos desenhado uma estrutura sujeita a três carregamentos, uma carga de e dois torques de . Considerando apenas os efeitos do esforço torsor, determine o valor do cisalhante máximo que ocorre no ponto A da nossa barra.
Passo 1
Podemos ver nessa questão que o nosso objetivo principal é determinar o valor do cisalhante máximo, antes de qualquer coisa devemos analisar, pelo enunciado, que devemos apenas considerar os efeitos do esforço torsor, logo só usaremos a fórmula
Porém também sabemos que queremos o cisalhante máximo, e para termos o cisalhante máximo devemos fazer pois para os efeitos do torsor os pontos mais extremos possuem os maiores cisalhantes.
Passo 2
Outra coisa que precisamos calcular é o nosso momento polar de inercia (). Aqui vale lembrar que o nosso momento polar de inercia é sempre da seção. Como no enunciado nos é dito que se trata de uma seção circular, usaremos como momento polar de inercia a equação
Substituindo na nossa equação principal, teremos que
Passo 3
O raio definimos facilmente, porém devemos tomar cuidado com o torsor, pois esse se trata do torsor máximo que está agindo na nossa peça, para descobrirmos o seu valor faremos a seguinte sequência de passos.
Primeiro cortamos a nossa barra no ponto que desejamos calcular o torsor
Em seguida levamos até essa seção todos os esforços que tínhamos antes de cortar e que após o corte não estamos vendo mais. Como só nos interessa analisar efeitos do torsor, podemos levar os nossos 2 torques de diretamente para seção.
Também temos que levar os esforços torsores causados pela carga de . Para calcular o seu valor precisamos analisar o seu braço de alavanca, olhando a figura abaixo teremos que
Trocando a nossa carga pelo efeito torsor causado por ela teremos que
Levando esse esforço para nossa seção A teremos que
Logo também já temos o nosso torsor que age na peça que é dado por
Passo 4
Agora que já temos tudo que precisamos, basta substituir e determinar o valor do nosso cisalhante máximo
Substituindo teremos que
Resposta
Exercício Resolvido #7
Elaboração própria
Abaixo é mostrado um eixo maciço e circular de diâmetro 200mm de uma barra de aço. Essa barra possui . Sabendo disso e ainda que há uma carga de 10 KN que contribui na torção, determine o valor máximo de sem que haja rompimento da barra. Analise apenas as contribuições referentes aos esforços torsores.
Passo 1
Podemos ver nessa questão que o nosso objetivo principal é determinar o valor do torque máximo, antes de qualquer coisa devemos analisar, pelo enunciado, que devemos apenas considerar os efeitos do esforço torsor, logo só usaremos a fórmula
Porém também sabemos que queremos o torque máximo, e para termos o torque máximo devemos fazer pois para os efeitos do torsor os pontos mais extremos possuem os maiores cisalhantes.
Passo 2
Outra coisa que precisamos calcular é o nosso momento polar de inercia (). Aqui vale lembrar que o nosso momento polar de inercia é sempre da seção. Como no enunciado nos é dito que se trata de uma seção circular, usaremos como momento polar de inercia a equação
Substituindo na nossa equação principal, teremos que
Passo 3
O que precisamos saber agora é que queremos o valor máximo do nosso torque sem que haja rompimento. Para garantirmos isso devemos fazer
Agora a única coisa que falta é determinarmos o torsor máximo que está atuando na nossa peça.
Passo 4
Para determinar o torsor devemos tomar alguns cuidados. O primeiro é que temos duas contribuições para os nossos torsores. Uma é o próprio T máximo que queremos determinar, a outra é a carga de 10 KN que produzirá o torsor mostrado na figura abaixo.
Logo podemos definir o nosso torsor como
Passo 5
Vamos resolver a nossa fórmula então
Sabemos que
E o torque deixamos para calcular por último.
Substituindo teremos que
Isolando o valor de T teremos que
Mas devemos lembrar que
Como acabamos de descobrir o valor do torque que podemos aplicar ao todo, basta descobrirmos qual o valor do torque parcial que podemos aplicar.
Substituindo teremos que
Logo contando com os torsores aplicados, o maior torque que poderia ser dado nessa peça seria de 105,7 KN.m.
Resposta
Exercício Resolvido #8
Elaboração própria
A barra de madeira abaixo representa o eixo de giro de um moinho. Por problemas nas engrenagens uma das extremidades do eixo ficou presa. Sabendo que o eixo foi sujeito aos esforços torsores mostrados abaixo e que a resistência ao cisalhamento dessa barra (levando em consideração apenas esforços torsores) é de 25 Mpa, determine o raio máximo que a nossa barra poderá ter para que o eixo não rompa.
Passo 1
Podemos ver nessa questão que o nosso objetivo principal é determinar o valor do raio máximo, antes de qualquer coisa devemos analisar, pelo enunciado, que devemos apenas considerar os efeitos do esforço torsor, logo só usaremos a fórmula
Porém também sabemos que queremos o torque máximo, e para termos o torque máximo devemos fazer pois para os efeitos do torsor os pontos mais extremos possuem os maiores cisalhantes.
Passo 2
Outra coisa que precisamos calcular é o nosso momento polar de inercia (). Aqui vale lembrar que o nosso momento polar de inercia é sempre da seção. Como no enunciado nos é dito que se trata de uma seção circular, usaremos como momento polar de inercia a equação
Substituindo na nossa equação principal, teremos que
Passo 3
O que precisamos saber agora é que queremos o valor máximo do nosso raio sem que haja rompimento. Para garantirmos isso devemos fazer
Agora a única coisa que falta é determinarmos o torsor que está atuando na nossa peça.
Passo 4
Para determinarmos o torsor que está agindo na nossa peça, vamos ir trocando cada braço de alavanca pela ação de um torsor ligado a ele, com isso teremos que
Podemos ver que a barra de baixo dará a mesma contribuição da barra de cima
Colocando também as contribuições laterais teremos que
Logo podemos definir o nosso torsor como
Passo 5
Vamos resolver a nossa fórmula então
Sabemos que
Substituindo teremos que
Isolando o valor de T teremos que