Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 30

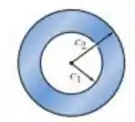
(a) Para uma dada tensão de cisalhamento admissível, determine a relação T / w do torque T máximo admissível e o peso da unidade de comprimento w para o eixo vazado mostrado na figura. (b) Chamado de T / w 0 o valor dessa relação para uma seção transversal cheia com o mesmo raio c 2 , expresse a relação T / w para o eixo vazado em termos de T / w 0   e c 1 / c 2 .

Passo 1

E aí gurizada tudo belezinha? Primeiramente para podermos relacionar partimos que:

p = P L = ρ g L A L = ρ g A = ρ g π c 2 2 - c 1 2

Onde:   p = p e s o   p o r   u n i d a d e   d e   c o m p r i m e n t o ,   ρ g =   p e s o   e s p e c í f i c o ,   P = p e s o   t o t a l e L = c o m p r i m e n t o

T = j τ c 2 = π 2 c 2 4 - c 1 4 c 2 τ a l l = π 2 c 2 2 + c 1 2 c 2 2 - c 1 2 c 2 τ

Passo 2

Então temos que:

T P = c 1 2 + c 2 2 τ

T P = c 1 2 + c 2 2 τ 2ρg c 2 eixo vazado

Onde:

c 1 =0 para o eixo sólido

Então temos:

T p 0 = c 2 τ 2ρg eixo sólido

Passo 3

Então para o eixo vazado a relação de T/w fica:

T/ p h T/ p 0 =1+ c 1 2 c 2 2 T p = T p 0 1+ c 1 2 c 2 2

Resposta

Gurizada, como percebemos a relação de para ( torque e o peso de unidade de comprimento)do eixo vazado é de:

T p = c 1 2 + c 2 2 τ all 2ρg c 2 eixo vazado

E o valor dessa relação para uma seção transversal cheia com o mesmo raio c 2 , novamente para o eixo vazado é:

T p = T p 0 1+ c 1 2 c 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O conjunto é composto por duas seções de tubo de aço galvanizado interligadas por uma redução em B . O tubo menor tem diâmetro externo de 18,75mm e diâmetro interno de 17mm , enquanto o tubo maior tem
O eixo tem diâmetro externo de 32mm e diâmetro interno de 25mm . Se for submetido aos torques mostrados na figura, determine a tensão de cisalhamento máxima absoluta desenvolvida no eixo. Os mancais l
O eixo maciço de 32mm de diâmetro é usado para transmitir os torques aplicados às engrenagens. Se o eixo estiver apoiado em mancais lisos em A e B , que não resistem a torque, determine a tensão de ci
O eixo maciço com 60mm de diâmetro está sujeito aos carregamentos de torção distribuídos e concentrados mostrados na figura. Determine as tensões de cisalhamento máxima e mínima no eixo e especifique
O tubo de cobre tem diâmetro externo de 62,5mm e diâmetro interno de 57,5mm . Se estiver firmemente preso à parede em C e for submetido a um torque uniformemente distribuído, como mostra a figura, det