Ângulo de Torção e Problemas Estaticamente Indeterminados
Produzido por Pablo RicardoTeoria
Introdução
Vamos dizer que seu professor/sua professora chegou em aula e lançou o seguinte desafio:
Determine as reações em e em no eixo abaixo, sendo que os trechos e são feitos de materiais diferentes e possuem comprimentos e diâmetros diferentes:
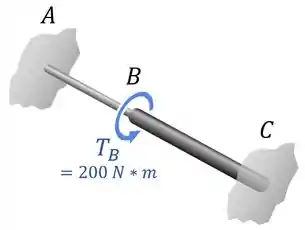
Aí a gente pensa...
Poxa, se tem um torque no sentido anti-horário aplicado em , as paredes em e em vão reagir com torques no sentido horário para manter a peça toda em equilíbrio.
Pensando nisso e usando a regra da mão direita, a gente consegue fazer o diagrama de corpo livre abaixo desse eixo:
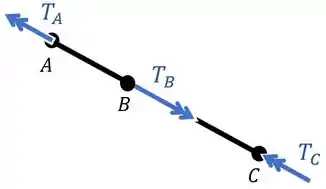
E aí aqui a gente encontra um problema.
Nós temos dois torques desconhecidos que queremos encontrar: e .
Mas só temos uma equação de equilíbrio: o equilíbrio de torques ().
Ele nos diz que , mas isso não é suficiente para que a gente encontre os dois torques desconhecidos.
Ou seja, esse é um problema estaticamente indeterminado: os métodos da estática (diagrama de corpo livre e equações de equilíbrio) não são suficientes para resolver ele.
Então...
Como é que a gente pode fazer para encontrar as reações nesse caso?

A solução disso se chama equação de compatibilidade. E vai utilizar o conceito de ângulo de torção!
Ângulo de torção
A gente pode definir como o ângulo de torção entre duas seções de um eixo:
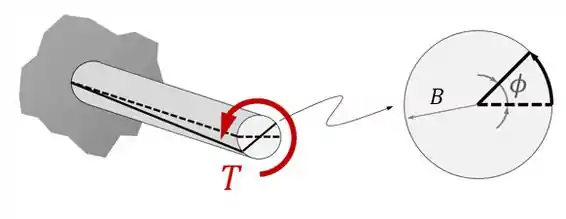
A boa notícia é que existe uma fórmula que descreve os ângulos de torção em um eixo (ou em um trecho de um eixo) em função dos torques que atuam nele!
É a fórmula do ângulo de torção:
Onde:
- é o ângulo de torção do trecho em radianos;
- é o torque interno no trecho, e pode ser encontrado como uma função dos torques aplicados no eixo através de uma análise dos esforços internos;
- é o comprimento do trecho;
- é o módulo de elasticidade transversal do material de que é feito o trecho e é normalmente dado em ;
- é o momento polar de inércia da seção transversal do trecho e é calculado usando as fórmulas que já vimos quando estudamos a Fórmula da Torção.
Equação de compatibilidade
Vamos entender agora a solução do problema!!
Um equação de compatibilidade é quando a gente relaciona as deformações nas peças de forma a garantir que elas respeitem a geometria do lugar onde elas estão.
Por exemplo, no nosso caso, nós temos duas paredes em e em que nem andam nem giram: elas estão fixas.
Só que e são 100% fixos lembra disso? Então o ângulo de torção nesses pontos é zero!
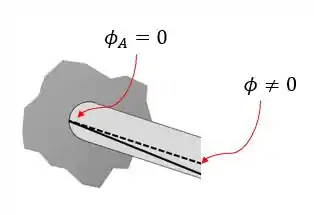
Olha como na parede é realmente zero, enquanto um outro genérico é diferente de zero! Logo:
Além disso, nós podemos dizer que o ângulo relativo entre os pontos e () é zero também!
Agora, o nosso eixo é feito dos trechos e . Se a gente for visualizar o ângulo vai ficar assim:
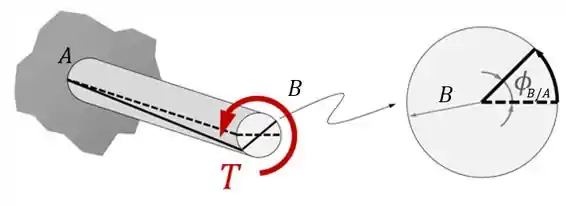
Nãoi mudou muita coisa né? Isso porque o ponto tem ângulo de troção nula!
Show! Mas a gente pode fazer a mesma coisa para vai ficar assim:
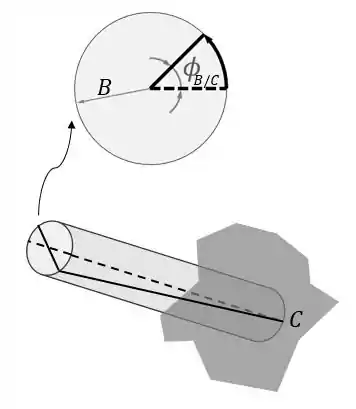
Então o ângulo de torção entre e é igual a soma dos ângulos de torção de cada trecho:
Essa é a nossa equação de compatibilidade! A gente pode visualizar a equação como um todo da seguinte forma:
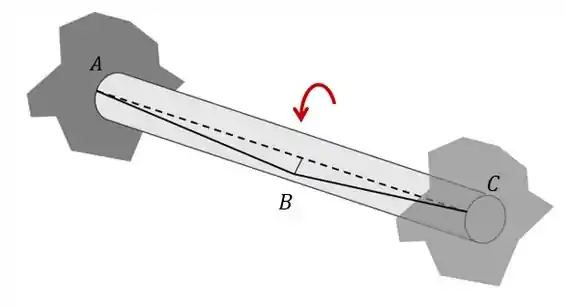
Olha como o ponto rotacionou, enquanto os outros dois pontos permaneceram estáticos!
Se conseguimos descrever os ângulos de torção e no nosso eixo em função dos torques que atuam nele, vamos ter uma segunda equação relacionando os torques no eixo.

Juntando essa segunda equação com a equação vinda do equilíbrio de torques, vamos conseguir determinar os torques e desconhecidos!
Então, por exemplo, aplicando a fórmula do ângulo de torção para os trechos e do nosso eixo e substituindo isso na equação de compatibilidade , vamos ter que:
Exemplo
Vamos fazer um exercício então! Imagine que temos uma barra de aço engastada como na figura a seguir. Se um torque de for aplicado na extremidade livre da barra, qual será o ângulo de torção nos pontos e no ponto médio da barra? Sabe-se que a barra tem diâmetro igual a .
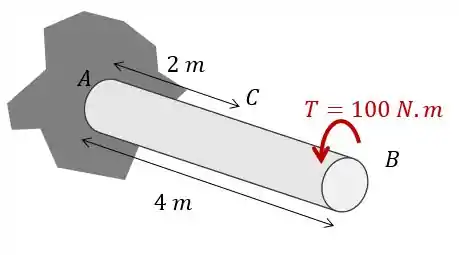
A primeira coisa que a gente já pode responder é que o ângulo de torção é zero no ponto engastado . Isso até mesmo se justifica pela equação já que
Show! Essa foi fácil. Agora vamos ver para a extremidade livre, o ponto onde . Visualmente vai ficar assim:
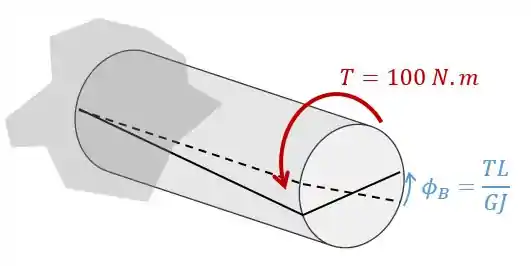
A gente tem a distância e o torque . depende do material e para o aço vale e o momento polar de inércia para uma seção circular é calculado como:
Para o nosso caso:
Substituindo na equação nós vamos ter:
E para o ponto ? Pessoal, a única coisa que muda de para é o comprimento que cai pela metade então podemos dizer que:
Repara que se existir apenas um torque então a variação segue um padrão linear!!
Conversão para Graus
Caso seja necessário fazer a conversão do ângulo de torção , calculado pela sua fórmula em radianos, para graus (), basta lembrar que equivale à , de tal forma que:
Semelhanças com a Variação de Comprimento
Uma das formas de decorar essa fórmula é pensar nas semelhanças entre ela e a fórmula da variação de comprimento lá de carga axial:
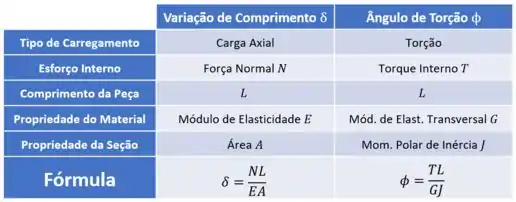
Além disso, semelhanças também existem na forma como as equações de compatibilidade são escritas.
Se um exercício de carga axial com uma folga de entre duas peças e tinha uma equação de compatibilidade:
Um exercício equivalente de torção, mas com uma folga de , vai ter uma equação de compatibilidade:
Um Comentário Final
Caso você tenha um eixo com um torque distribuído ou com uma seção transversal que varia continuamente (como um cone, por exemplo), você deve usar a fórmula:
Que é a fórmula geral do ângulo de torção.
Em todos os outros casos, o ângulo de torção de um eixo pode ser calculado somando os ângulos de torção de cada um dos seus trechos.
Ângulo de torção
Equação de compatibilidade
Exemplo
Semelhanças com a Variação de Comprimento
Um Comentário Final
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria.
Um eixo maciço de aço () possui um comprimento e um raio . Ele está submetido em suas extremidades a um torque . Determine o valor do ângulo de torção nesse eixo devido ao torque aplicado.
Forneça o resultado em graus ().
Passo 1
O que está acontecendo?
O eixo possui um módulo de elasticidade transversal , um comprimento , um raio e está submetido a um torque .
Além disso, ele é maciço, de tal forma que o seu momento de inércia polar vai ser dado pela fórmula:
E o que é que o exercício quer?
Ele quer que a gente determine o ângulo de torção nesse eixo, que deve ser calculado através de sua fórmula:
Passo 2
Então para calcular o ângulo de torção no eixo, aplicamos a sua fórmula:
De início, podemos substituir que .
Assim temos que:
Arrumando essa expressão, ela fica assim:
Agora, podemos substituir os valores:
- ;
- ;
- ;
- & ,
Para encontrar que:
O que dá:
Passo 3
Agora, esse resultado que encontramos a partir da fórmula do ângulo de torção está em radianos.
Para responder o nosso exercício, precisamos converter esse resultado para graus.
Para tanto, podemos nos lembrar que:
O que significa que:
Usando isso, o nosso resultado vai ficar assim:
Calculando tudo, encontramos a nossa resposta final:
Resposta
Exercício Resolvido #2
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 179-3.36.
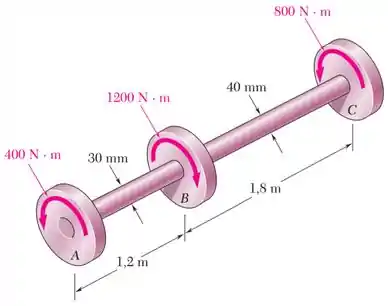
Os torques mostrados são aplicados nas polias , e . Sabendo que ambos os eixos têm seção transversal cheia e são feitos de latão (), determine o ângulo de torção entre e e e .
Passo 1
O que está acontecendo?
O eixo é composto pelos segmentos:
- , de comprimento , diâmetro , e, consequentemente, raio ;
- & , de comprimento , diâmetro , e, consequentemente, raio .
Ambos os segmentos são feitos de latão, com um módulo de elasticidade transversal .
Além disso, eixo é carregado com torques externos nos seus pontos , e , como mostra o seu DCL (diagrama de corpo livre) abaixo, feito utilizando a regra da mão direita:

A partir desse DCL, é possível fazer uma análise dos esforços internos para descobrir o valor dos torques internos e nos segmentos e do eixo, respectivamente.
E o que é que o exercício quer?
Ele quer que a gente determine o ângulo de torção entre os pontos e () e entre os pontos e ().
Para calcular , que é o ângulo de torção do segmento do eixo, podemos usar a fórmula do ângulo de torção:
Além disso, também podemos usar essa fórmula para calcular o ângulo de torção do segmento do eixo, .
Daí que, somando com , vamos encontrar :
Passo 2
Vamos começar o exercício fazendo uma análise dos esforços internos na peça para identificar os valores dos torques internos nos trechos e , e .
Primeiro, fazemos seções dentro desses trechos e desenhamos os torques internos desconhecidos:
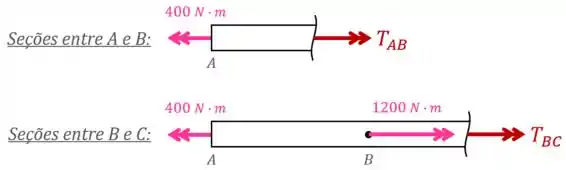
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Em seguida, aplicamos o equilíbrio de torques para cada trecho:
Isolando os torques desconhecidos e nessas equações, encontramos que:
Passo 3
Agora, podemos calcular os ângulos de torção dos segmentos e usando a fórmula:
Primeiro, temos que ambos esses segmentos possuem seções circulares maciças, e assim, tem um momento de inércia polar .
Usando isso, temos que:
Arrumando tudo, isso fica assim:
Agora, aplicando essa expressão para o segmento , temos:
Substituindo:
- ;
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
Encontramos que:
O que nos dá a resposta do item :
Já aplicando a expressão para o segmento , temos:
Substituindo:
Encontramos que:
Passo 4
Encontrados e , podemos soma-los para encontrar :
Substituindo os valores encontrados, temos que:
Calculando isso, encontramos a nossa resposta para o item :
Passo 5
Apesar de que o exercício não especificou no enunciado que ele queria os resultados em graus () e não em radianos (), ele forneceu o gabarito final em graus.
A verdade é que muitos professores preferem resultados em graus, então precisamos saber fazer essa conversão.
Lembra aí...
Você pode converter radianos para graus usando a relação de que equivale à :
Ou seja:
Substituindo isso nas nossas respostas, vamos ter que:
Calculando tudo, encontramos as nossas respostas finais:
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 153-5.73.
O eixo de aço A-36 tem diâmetro de e está preso nas extremidades e . Se for submetido ao momento, determine a tensão de cisalhamento máxima nas regiões e do eixo.
Dados: .
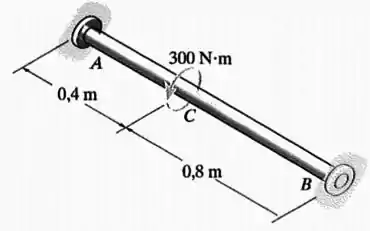
Passo 1
O que está acontecendo?
O eixo tem um módulo de elasticidade transversal , um diâmetro e, consequentemente, um raio .
Ele está submetido a um torque no ponto .
E ele está preso nas extremidades e , que realizam torques de reação nele de forma a manter o seu equilíbrio.
Usando a regra da mão direita, obtemos o seguinte DCL (diagrama de corpo livre) para esse eixo:

Aplicando as condições de equilíbrio nesse eixo, vamos ter uma única equação (equilíbrio de torques), mas duas incógnitas ( e ).
Isso significa que esse é um problema estaticamente indeterminado.
Então também vamos precisar de uma equação de compatibilidade para resolver o exercício.
Qual vai ser a equação de compatibilidade nesse caso?
Nesse caso, temos que o eixo está fixo nos pontos e .
Assim, temos que o ângulo de torção entre esses dois pontos deve ser igual à zero:
Mas o ângulo de torção entre esses dois pontos é igual à soma dos ângulos de torção do trecho e do trecho :
Essa vai ser a nossa equação de compatibilidade.
Para que ela seja útil, vamos precisar descrever os ângulos de torção de cada trecho do eixo usando a fórmula:
E o que é que o exercício quer?
Ele quer saber a tensão de cisalhamento máxima nas regiões e do eixo.
Essas tensões máximas podem ser calculadas usando a fórmula da torção:
Mas... para poder usar essas fórmulas, precisamos antes conhecer os torques internos nos trechos e desse eixo.
E para conhecer esses torques, vamos ter que usar o equilíbrio de torques e a equação de compatibilidade acima.
Passo 2
Então vamos começar o exercício identificando os torques internos nos trechos e do eixo.
Começamos pelo DCL do eixo:

Em seguida, fazemos uma análise dos esforços internos: secionamos o eixo em cada trecho e observamos os esforços internos nessas seções.
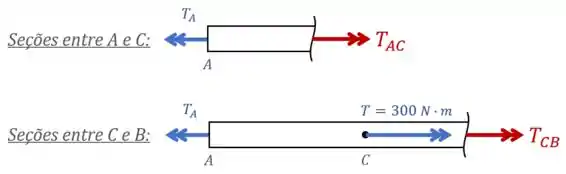
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Aplicando o equilíbrio de torques em cada caso, temos que:
Isolando os torques e , encontramos que:
Passo 3
Agora que já definimos os torques internos e nos diferentes trechos do nosso eixo, podemos estudar a nossa equação de compatibilidade:
Aplicando a fórmula do ângulo de torção para cada trecho, e tendo em mente que os dois trechos possuem:
- O mesmo módulo de elasticidade transversal ;
- E a mesma seção transversal circular maciça de raio , e, consequentemente, o mesmo momento de inércia polar ,
Essa equação fica assim:
Multiplicando tudo por , temos que:
Substituindo e :
E fazendo as multiplicações, temos que:
Colocando em evidência, isso fica assim:
E, finalmente, isolando , encontramos que:
Substituindo e , isso nos diz que:
Assim, temos que os torques internos e no nosso eixo são:
Passo 4
Por fim, agora que já conhecemos os torques e resistido por cada trecho do eixo, podemos calcular as tensões de cisalhamento máxima em cada trecho.
Para tanto, usamos a fórmula da torção:
Para ambos os trechos do eixo, que são ambos maciços e de raio , o momento polar de inércia vai ser igual à .
Dessa forma, temos que:
Simplificando, isso fica assim:
Aplicando essa expressão para o trecho , temos:
Substituindo , temos:
Finalmente, substituindo os valores:
- ;
- & ,
- ;
- & ,
Encontramos que:
Agora, como , isso significa que:
Fazendo o mesmo procedimento para , temos:
Substituindo , temos:
Por fim, substituindo os valores:
Encontramos que:
Como para a nossa resposta, só importa a intensidade da tensão de cisalhamento máxima , retiramos o sinal de negativo na hora de fornecer a nossa resposta final:
E assim finalizamos o exercício!
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 149-5.66.
O dispositivo serve como uma mola de torção compacta. É feito de aço A-36 e composto por um eixo interno maciço embutido em um tubo e acoplado a esse tubo por um anel rígido em . Podemos considerar que o anel em também é rígido e está preso de modo que não pode girar. Se a tensão de cisalhamento admissível para o material for e o ângulo de torção em estiver limitado a , determine o torque máximo que pode ser aplicado na extremidade .
Dados: .
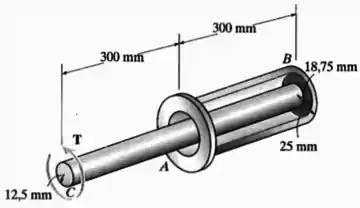
Passo 1
O que está acontecendo?
O eixo maciço possui um raio enquanto que o tubo possui um raio externo e um raio interno .
O eixo tem um comprimento enquanto que o tubo tem um comprimento .
Ambos possuem um módulo de elasticidade transversal .
E ambos estão submetidos ao mesmo torque , sendo que, a partir desse torque, é possível calcular:
1. Tanto a tensão de cisalhamento máxima em cada peça, usando a fórmula da torção:
2. Quanto o ângulo de torção em cada peça, usando a sua fórmula:
E o que é que o exercício quer?
Ele quer que a gente determine o torque máximo que pode ser aplicado nessa dispositivo, tendo em mente que:
1. A tensão de cisalhamento máxima tanto no tubo quando no eixo não pode ultrapassar a tensão de cisalhamento admissível :
& 2. O ângulo de torção em (), que é igual à soma dos ângulos de torção do tubo () e do eixo (), não pode ultrapassar o limite :
Passo 2
Vamos começar o exercício verificando as condições relativas à tensão de cisalhamento máxima:
Aplicando a fórmula da torção para o tubo e para o eixo (ambos submetidos ao mesmo torque ), essas condições acima ficam assim:
Como o tubo possui um raio externo e um raio interno , o seu momento de inércia polar vai ser:
Já para o eixo , maciço, vamos ter que:
Substituindo essas fórmulas nas expressões anteriores, vamos ter que:
Queremos avaliar qual é o torque máximo que pode ser aplicado, então devemos isolá-lo.
Fazendo isso, as nossas expressões ficam assim:
Ainda podemos arrumar essas expressões, deixando elas assim:
Agora, substituímos os valores:
- ;
- ;
- ;
- & ,
Para encontrarmos que:
Como esses números são muito grandes, podemos reescrevê-los em , encontrando assim as seguintes condições limitantes do torque :
Passo 3
Agora, vamos verificar a condição referente aos ângulos de torção:
Aplicando a fórmula do ângulo de torção para o tubo e para o eixo (ambos submetidos ao mesmo torque ), essa condição acima fica assim:
Colocando em evidência, temos que:
E isolando o torque , encontramos que:
Substituindo as fórmulas dos momentos polares de inércia , já definidas no passo anterior, isso tudo fica assim:
Sim, isso está meio assustador...

Mas não é nada que uma arrumadinha não resolva.
Dá para colocar o em evidência, por exemplo:
E aí multiplicar essa expressão por esse termo invertido, ou seja, por :
E pronto, já ficou um pouco melhor a cara da expressão!
Agora, a tentação é substituir os valores:
- ;
- ;
- ;
- ;
- ;
- ;
- & ,
E encontrar o valor máximo para o torque .
Mas a verdade é que ainda não podemos fazer isso.
Isso porque não podemos usar o valor .
Se usarmos ele, o nosso resultado final para vai sair em uma unidade bizarra como (graus).
Precisamos converter esse valor de para radianos!
Para fazer isso, multiplicamos ele por :
E encontramos que:
Agora sim, podemos substituir e calcular tudo.
Fazendo isso, vamos encontrar que:
Para deixar esse resultado em uma unidade mais usual, reescrevemos ele em , encontrando assim a nossa terceira e última condição limitante para o torque :
Passo 4
Comparando as três condições encontradas, vemos que a condição mais limitante é a condição :
Dessa forma, temos que o maior torque que pode ser aplicado no ponto do dispositivo desse exercício é:
Resposta
Exercício Resolvido #5
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 183-3.53.
O eixo composto mostrado consiste em uma jaqueta de latão de de espessura () unido a um núcleo de aço de de diâmetro (). Sabendo que o eixo está submetido a um torque de , determine a tensão de cisalhamento máxima na jaqueta de latão, a tensão de cisalhamento máxima no núcleo de aço e o ângulo de torção de relativo a .
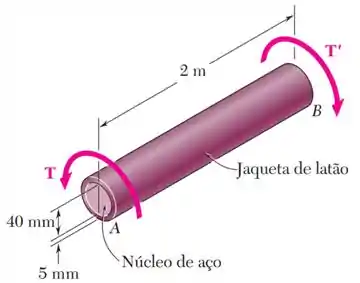
Passo 1
O que está acontecendo?
A jaqueta de latão tem:
- Um diâmetro interno de , e, consequentemente, um raio interno ;
- Uma espessura , e, consequentemente, um raio externo ;
- E um módulo de elasticidade transversal .
Já o núcleo de aço tem:
- Um diâmetro de , e, consequentemente, um raio ;
- E um módulo de elasticidade transversal .
Ambas as peças possuem um comprimento e estão suportando, juntas, a um torque de .
Como as peças estão suportando esse torque juntas, temos que a soma dos torques suportados pela jaqueta de latão e pelo núcleo de aço deve ser igual ao torque total:
Mas essa relação não é suficiente para que a gente possa determinar os valores dos torques e suportados por cada peça.
Então vamos ter que recorrer a uma equação de compatibilidade.
Qual vai ser a equação de compatibilidade nesse caso?
Nesse caso, temos que a jaqueta de latão e o núcleo de aço se torcem juntos.
Dessa forma, eles vão possuir o mesmo ângulo de torção :
Essa vai ser a nossa equação de compatibilidade.
Para que ela seja útil, vamos ter que aplicar, para cada peça, a fórmula do ângulo de torção:
Assim, vamos poder usar a equação de compatibilidade para relacionar os torques e .
E o que é que o exercício quer?
Nos itens e , ele quer saber as tensões de cisalhamento máximas na jaqueta de latão e no núcleo de aço, respectivamente.
Para calcular essas tensões, vamos primeiro encontrar os torques e suportados por cada peça, para, em seguida, aplicar a fórmula da torção:
Já no item , ele quer saber o ângulo de torção do conjunto, que vai ser igual tanto ao ângulo de torção do latão quando ao ângulo de torção do aço:
Assim, podemos escolher entre calcular ou para determinar o ângulo de torção do conjunto.
Passo 2
Então como vimos, do equilíbrio de torques, temos que:
Mas essa relação não é suficiente para calcular os torques desconhecidos e .
Então...
Vamos recorrer à equação de compatibilidade:
Aplicando a fórmula do ângulo de torção para o latão e para o aço (e tendo em mente que ambas as peças tem o mesmo comprimento ), isso fica assim:
Cortando com , temos que:
E isolando , encontramos que:
Agora, da Equação 1, temos que .
Sendo assim, temos que:
Em seguida, passando para o outro lado:
E colocando em evidência:
Encontramos que:
Agora, podemos identificar que:
- A jaqueta de latão vai ter um momento de inércia polar ;
- Enquanto que, para o núcleo de aço, que é maciço, .
Dessa forma, temos que:
Cortando com , isso significa que:
Finalmente, substituindo os valores:
- ;
- e ;
- & , e ,
Vamos encontrar que:
E como da Equação 1, temos que:
Podemos substituir e para encontrarmos que:
Passo 3
Agora que já conhecemos os torques e em cada peça, já podemos calcular as tensões de cisalhamento máxima em cada uma delas.
Para tanto, usamos a fórmula da torção:
Aplicando essa fórmula para a jaqueta de latão, vamos ter que:
Substituindo , isso fica assim:
Arrumando tudo, temos que:
Por fim, substituindo:
- ;
- & ,
- ;
- & ,
Encontramos que:
E como , isso significa que:
O que é a nossa resposta para o item !
Agora, aplicando a mesma fórmula, mas para o núcleo de aço, temos que:
Substituindo , isso fica assim:
E simplificando tudo, temos que:
Finalmente, substituindo:
Encontramos nossa resposta para o item :
Passo 4
Agora só falta o item : calcular o ângulo de torção.
Para tanto, vamos optar por calcular o ângulo de torção no núcleo de aço:
Aplicando a fórmula do ângulo de torção para o núcleo de aço, que possui um comprimento , temos que:
Como o núcleo de aço tem seção transversal circular e maciça de raio , temos que , de tal forma que:
Agora, substituindo os valores:
- ;
- ;
- ;
- & ,
Vamos encontrar que:
Multiplicando esse resultado por , conseguimos convertê-lo para graus:
Calculando tudo, encontramos nossa resposta para o item e finalizamos o exercício:
Resposta
Exercício Resolvido #6
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 183-3.57.
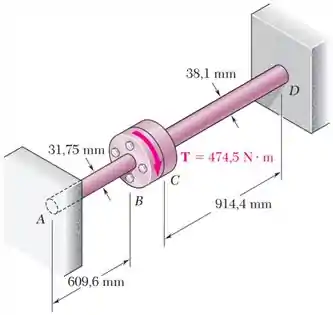
Dois eixos sólidos de aço são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimensionados de modo que permitam uma rotação relativa entre as flanges de até antes que ambas passem a girar juntas.
Sabendo que , determine a máxima tensão de cisalhamento em cada eixo quando um torque de intensidade igual a é aplicado na flange .
Passo 1
O que está acontecendo?
Os eixos maciços e tem diâmetros e , e, consequentemente, raios e .
Além disso, eles têm comprimentos e e o mesmo módulo de elasticidade transversal .
Um torque é aplicado em e, para manter o equilíbrio das peças, as paredes aplicam torques de reação e em e .
Usando a regra da mão direita, podemos fazer um DCL (diagrama de corpo livre) para visualizar todos esses torques:

Agora...
Fazendo o equilíbrio de torques no DCL acima, vamos encontrar que:
Mas essa relação não é suficiente para que a gente saiba o valor dos torques e , então vamos ter que recorrer a uma equação de compatibilidade.
E qual vai ser a equação de compatibilidade nesse caso?
Então...
Lá em “Carga Axial”, talvez você tenha resolvido alguns exercícios em que haviam folgas entre as peças.
Lá, quando a gente tinha duas peças entre duas paredes e uma folga entre as peças, tínhamos que:
Ou seja, a nossa equação de compatibilidade era:
Agora, temos mais uma vez duas peças entre duas paredes e uma folga entre essas peças.
Mas dessa vez, temos um problema de torção.
Então ao invés de variações de comprimento , vamos ter ângulos de torção :
Como no nosso caso a peça 1 é o eixo , a peça 2 é o eixo e a folga é de , a nossa equação de compatibilidade vai ser:
Sendo que os ângulos de torção podem ser descritos pela sua fórmula:
E o que é que o exercício quer!?!??
Ele quer que a gente calcular as tensões de cisalhamento máximas em cada eixo, que vão ser dadas pela fórmula da torção:
Agora, para calcular essas tensões em cada eixo, vamos ter que:
1. Identificar quais são os torques internos nos eixos e ;
& 2. Usar a equação de compatibilidade para calcular esses torques internos .
Passo 2
Então vamos começar identificando os torques internos em cada eixo.
Começamos pelo DCL do conjunto:

E em seguida fazemos uma análise dos esforços internos: secionamos o conjunto em seus diferentes trechos e observamos os esforços internos nas seções.
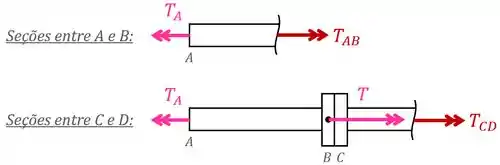
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Aplicando o equilíbrio de torques para cada caso, temos que:
E isolando os torques internos e , encontramos que:
Passo 3
Agora que já identificamos os torques internos, já podemos desenvolver a nossa equação de compatibilidade:
Aqui, vamos aplicar a fórmula do ângulo de torção para calcular os ângulos e .
Mas a fórmula do ângulo de torção fornece resultados em radianos ().
Então antes de tudo, vamos converter a folga de para radianos.
Para tanto, multiplicamos ela por :
Calculando tudo, encontramos que:
Agora sim, podemos aplicar a fórmula do ângulo de torção para os eixos e , ambos de mesmo módulo de elasticidade transversal :
Como os eixos e são maciços, podemos substituir para eles.
Além disso, podemos substituir que e que .
Fazendo tudo isso, temos que:
Em seguida, podemos tirar em evidência:
E passar esse termo para o outro lado:
Podemos arrumar a equação para deixa-la assim:
E colocar em evidência:
E, finalmente, podemos isolar , para encontrar que:
Agora, substituímos os valores:
- ;
- ;
- e ;
- & e ,
Para encontrarmos o valor de :
Sendo que esse valor poder ser reescrito em :
Passo 4
Conhecendo , podemos agora fazer o cálculo dos valores dos torques internos e nos eixos.
Primeiro, temos que:
Como , isso significa que:
Em seguida, temos que:
Como e , isso significa que:
O que dá:
Passo 5
Calculados os torques internos, podemos calcular as tensões de cisalhamento máximas em cada eixo.
Para tanto, vamos usar a fórmula da torção:
Como os dois eixos são maciços, temos que para ambos.
Dessa forma, temos que:
Arrumando tudo, isso fica assim:
Aplicando essa fórmula para os eixos e , vamos ter:
Em seguida, substituindo os valores:
- ;
- ;
- ;
- & ,
Encontramos que:
Por fim, antes de escrevermos a nossa resposta final, podemos perceber duas coisas.
Primeiro, que ao querer saber qual é a tensão de cisalhamento máxima em cada eixo, o exercício só quer saber a intensidade de .
Então podemos retirar o sinal de negativo de .
E segundo, que é o mesmo que .
Tendo tudo isso em mente, definimos a nossa resposta final:
Resposta
Exercício Resolvido #7
Elaboração própria
A barra de madeira abaixo está sujeita aos esforços de torção mostrados na figura. Com base nos seus conhecimentos de Resistencia dos materiais determine o valor das reações das paredes nos pontos A e D.
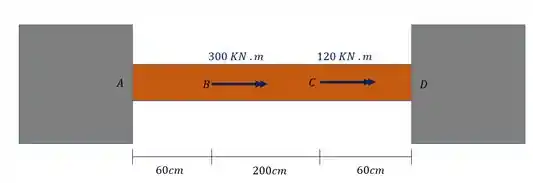
Passo 1
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá
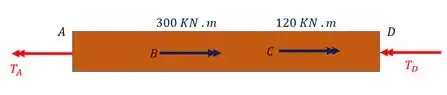
Fazendo o somatório de torques teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade, nesse caso, será o nosso ângulo de torção, dado por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação angular, ou seja, a deformação angular da nossa barra deve ser igual a deformação angular total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação angular total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação angular do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto o momento polar de inercia quanto o módulo de elasticidade transversal são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Então o que falta é apenas determinar o valor dos torques em cada trecho.
Passo 3
Como só falta determinar o torque, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro Torque do trecho AB
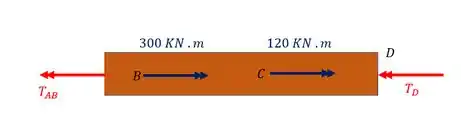
Fazendo o equilíbrio teremos que
Normal do trecho BC
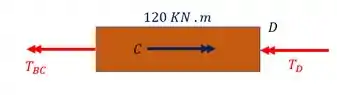
Fazendo o equilíbrio teremos que
Normal do trecho CD
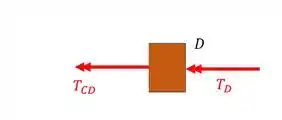
Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos cortar
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de
Resposta
Exercício Resolvido #8
Elaboração própria
A barra de aço da figura foi sujeita aos esforços de torção mostrado na figura. Sabendo que se trata de uma seção triangular com as dimensões mostradas, e que ainda a barra possui um modulo de elasticidade transversal de determine as reações da parede nesse caso.
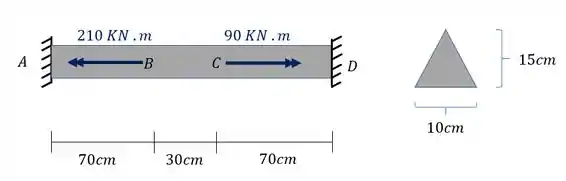
Passo 1
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá

Fazendo o somatório de torques teremos que
Como podemos ver temos duas incógnitas ( e uma única equação (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade, nesse caso, será o nosso ângulo de torção, dado por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação angular, ou seja, a deformação angular da nossa barra deve ser igual a deformação angular total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação angular total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação angular do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Sabemos que como a barra é homogênea, tanto o momento polar de inercia quanto o módulo de elasticidade transversal são iguais nos três trechos. Também sabemos facilmente determinar o valor de cada comprimento que é dado no desenho. Então o que falta é apenas determinar o valor dos torques em cada trecho.
Passo 3
Como só falta determinar o torque, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro Torque do trecho AB

Fazendo o equilíbrio teremos que
Normal do trecho BC
Fazendo o equilíbrio teremos que
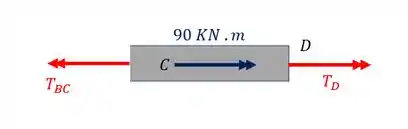
Normal do trecho CD
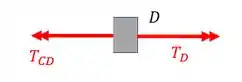
Fazendo o equilíbrio teremos que
Passo 4
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Podemos cortar , o que mostra que a nossa resposta em nada depende do tipo de seção que está sendo usada, logo a seção triangular em nada será usado aqui.
Isolando teremos que
Agora é só calcularmos o valor de
Passo 5
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de
Resposta
Exercício Resolvido #9
Elaboração própria
Na figura abaixo temos uma barra de madeira com seção retangular que varia conforme mostrado na figura. Usando seus conhecimentos relacionados a ângulo de torção, determine as deformações angulares em graus das seções A e B marcadas na figura.
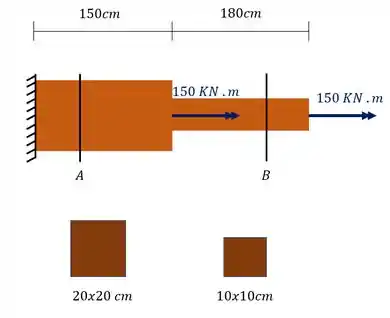
Passo 1
Como ele quer que determinemos o nosso ângulo de torção, precisaremos usar a nossa fórmula de deformação angular que é dada por
Olhando a nossa fórmula temos dois valores que determinamos facilmente
Um é o comprimento e o outro é o módulo de elasticidade transversal, chamando a barra mais fina de B e a mais grossa de A, teremos que
O modulo de elasticidade transversal é o mesmo para ambas, já que se trata do mesmo material, logo
Passo 2
Outra coisa que precisamos determinar é o momento polar de inercia, para isso temos que lembrar do seguinte conceito.
Vale ressaltar que essa relação só vale para os casos em que não ocorrer empenamento da nossa peça, se por acaso você fizer um exercício em que há empenamento da peça, essa relação não poderá ser usada.
Como para seções retangulares nos temos que
Teremos que o momento polar de inercia será
Como se trata de uma seção quadrada teremos que . Substituindo teremos que
Logo para menor seção teremos que
E para seção maior teremos que
Passo 3
Por fim basta apenas determinar o valor do momento torsor em cada uma das seções, dividindo a nossa barra na seção A teremos que

Para sabermos o torque que age nessa seção devemos levar até ela todos os esforços que sumiram após fazermos o corte, logo teremos que os esforços que agem nessa seção são
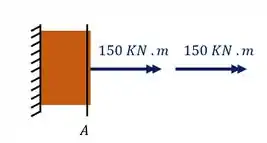
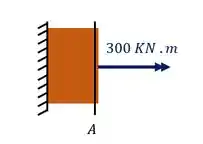
Logo na nossa seção A o toque atuante é
Agora dividindo a nossa barra na seção B teremos que
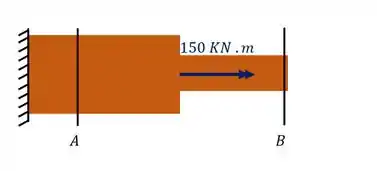
Para sabermos o torque que age nessa seção devemos levar até ela todos os esforços que sumiram após fazermos o corte, logo teremos que o esforço que age nessa seção é
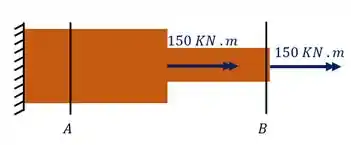
Logo na nossa seção B o toque atuante é
Passo 4
Como já temos os valores que precisávamos, basta substituirmos na nossa equação.
Temos que
Logo para nossa seção A teremos que
Também temos que
Mas calma, ao usar a fórmulinha, achamos o ângulo de em relação a . Logo para nossa seção B teremos que
Como queremos as nossas deformações angulares em graus teremos que fazer regra de 3
Fazendo isso teremos que
Aí para achar o ângulo de torção de em relação ao apoio (começo da barra), a gente o soma com o ângulo de :
Resposta
Exercício Resolvido #10
Elaboração própria
A barra abaixo está sujeita aos carregamentos mostrados. Sabendo que cada seção possui as dimensões e formatos mostrados abaixo da figura, determine o valor das reações da parede na situação mostrada.

Passo 1
Como podemos ver, nesse tipo de questão precisamos determinar as reações de apoio. Para determinarmos essas reações de apoio precisamos saber se o nosso problema é isostático ou se é um problema estaticamente indeterminado. Como temos duas paredes no nosso problema, podemos desconfiar que talvez seja a segunda opção.
Para termos certeza que se trata de um problema estaticamente indeterminado, precisamos definir o diagrama de corpo livre e fazer o balanceamento entre o número de incógnitas e o número de equações, então vamos lá

Fazendo o somatório de torques teremos que
Como podemos ver temos duas incógnitas ( e uma única equa��ão (), logo de fato se trata de um problema estaticamente indeterminado. Sabemos então, que para resolve-lo precisamos do que chamamos de equação de compatibilidade.
Passo 2
Temos que lembrar que a nossa equação de compatibilidade, nesse caso, será o nosso ângulo de torção, dado por
Mas onde ela será usada?
Ai que entra a nossa relação de deformação angular, ou seja, a deformação angular da nossa barra deve ser igual a deformação angular total máxima que ela pode ter, que pode ser dada por
O que precisamos saber primeiro: como as paredes são indeslocaveis a deformação angular total máxima possível para a nossa barra é zero, logo
O que devemos saber por segundo é que a deformação angular do trecho AD é composto de três parcelas, uma do trecho AB, uma do trecho BC e por fim do trecho CD. Logo podemos escrever a nossa equação de compatibilidade como.
Colocando tudo em termos do que já temos e também usando a nossa fórmula de deformação total teremos que
Passo 3
Outra coisa que precisamos determinar é o momento polar de inercia, para isso temos que lembrar do seguinte conceito.
Vale ressaltar que essa relação só vale para os casos em que não ocorrer empenamento da nossa peça, se por acaso você fizer um exercício em que há empenamento da peça, essa relação não poderá ser usada.
Como para seções retangulares nos temos que
Teremos que o momento polar de inercia será
Sabemos que
Substituindo teremos que
Para seções circulares sabemos que
Sabemos que
Substituindo teremos que
Para seções elípticas temos que
O momento polar de inercia será
Sabemos que
Substituindo teremos que
Passo 4
Como só falta determinar o torque, basta apenas que cortemos as barras e façamos o equilíbrio da nossa peça.
Primeiro Torque do trecho AB

Fazendo o equilíbrio teremos que
Normal do trecho BC

Fazendo o equilíbrio teremos que
Normal do trecho CD
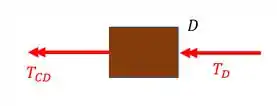
Fazendo o equilíbrio teremos que
Passo 5
Agora que já temos os valores dos normais vamos substituir na nossa equação
Agora vamos isolar os valores de
Isolando teremos que
Agora é só calcularmos o valor de
Passo 6
Sabemos que
Substituindo teremos que
Como já sabemos qual é a nossa primeira equação, basta substituir nela para descobrimos o valor de