Teoria
Introdução
Nos já vimos até aqui como definir uma viga e como resolve-la pelo método das integrais e pelo método do equilíbrio, agora, vamos analisar o caso que ocorre, na maioria das vezes, em pontes.
Algumas estruturas de pontes possuem trechos que permitem a rotação de parte da estrutura da ponte. Geralmente esses trechos são apoiados no que chamamos de dentes Gerber, e costumamos representar esses dentes através de rótulas, como mostra a figura abaixo, em que trocamos os dentes Gerber da ponte, por uma representação unifilar.
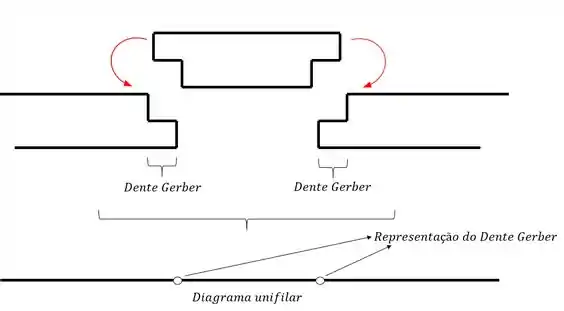
Método de solução
Pra resolver as vigas Gerber, é necessário tomar alguns cuidados, e seguir uma sequencia de solução que é a seguinte
- Devemos quebrar a viga Gerber de forma a ter vigas isostática menores e simples, que saberemos resolver
- Só podemos quebrar vigas Gerber nas Rótulas, desde que a quebra dessas rótulas forme vigas simples
- Cada rótula quebrada dará origem a um apoio fictício do segundo gênero, porém em vigas Gerber temos apenas cargas verticais, logo, sempre tomaremos que as reações horizontais dos apoios fictícios serão zero.
- Após a quebra definimos uma ordem de solução, sendo primeiro as mais externas e depois as mais internas.
- As reações dos apoios fictícios serão transferidas para a viga que esse apoio estiver apoiado, SEMPRE invertendo o sentido das reações calculadas, ou seja, se o apoio fictício possui reações pra cima, passará para as barras de baixo reações para baixo.
- Por fim, após resolver as barras que forem quebradas resolve as barras que receberem as reações dos apoios fictícios
- Vale relembrar que resolver uma viga, significa fazer o diagrama de cortante e momentos fletores dela.
Aqui em cima foi dado o passo a passo para resolvermos uma viga Gerber, vamos agora por a mão na massa e ver como se resolve na pratica esse tipo de viga.
Situação
A nossa situação não terá valores pois o nosso objetivo é apenas mostrar como dividimos a nossa viga Gerber em vigas simples. Depois que tivermos vigas simples, aí já sabemos resolver tanto pela aula de esforços internos em vigas que tá no assunto flexão quanto a aula de solução de vigas simples que está no assunto vigas, o objetivo dessa aula é então mostrar apenas como dividimos a viga, e nos exercícios nós partimos pra solução com valores mesmo. Então a nossa situação é a seguinte
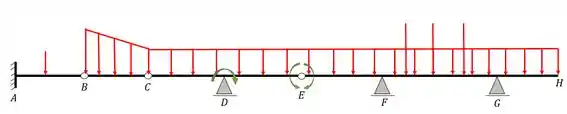

Eu sei que pode parecer muito complexo, mas vamos ver como na verdade é bem simples resolver esse tipo de questão, vamos lá então.
Passo 1: Quebrar as rótulas e descobrir quais formarão vigas simples
A primeira coisa que temos que fazer é quebrar as rótulas e, no lugar das rótulas colocar apoios fictícios. Se com os apoios fictícios todas as vigas ficarem simples e isostáticas, aí basta resolver, se não ficarem, tem que achar outras rótulas que vão formar vigas isostáticas e simples, no nosso caso o que teremos quando quebrarmos as rótulas é o seguinte;
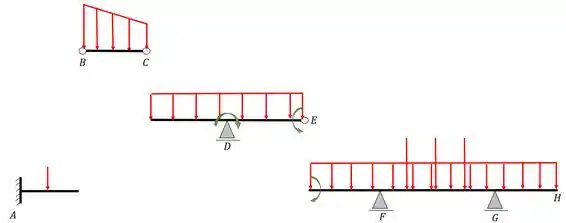
Perceba que todos os carregamentos pertencentes a cada barra permaneceram nas suas respectivas barras. Também veja que os dois momentos aplicados na rótula E foram divididos entre as barras, mas veja que eu ainda não coloquei os apoios fictícios nas rótulas quebradas, vamos colocar então.
Passo 2: Apoios fictícios nas rótulas quebradas
Como já foi dito antes, não consideraremos cargas horizontais na nossa viga, dessa forma, apenas teremos reações verticais dos nossos apoios, assim podemos por apoios fictícios representados da seguinte forma
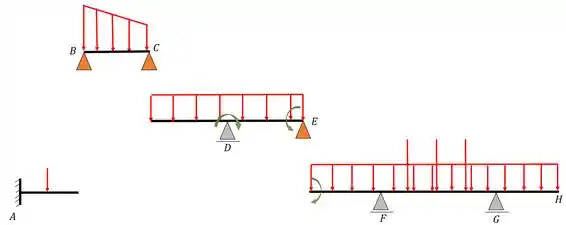
Perceba que todos os apoios marcados de laranja são rótulas que foram quebradas. Outra coisa que vale mostrar é que TODAS as barras são:
- Simples, então sabemos resolver todas elas
- Isostáticas, o que também nos permite resolver elas pelos métodos que já conhecemos
- Se todas as barras são simples e isostáticas, então dividimos as barras nas rótulas corretas e basta irmos para o próximo passo.
Mas antes de resolvermos precisamos saber como cada reação de apoio irá contribuir nas outras barras, e só depois, em fim, definir uma ordem de solução.
Passo 3: reações de apoio e sua contribuição
Sabemos que só teremos reações de apoio vertical, logo podemos trocar todos os nossos apoios pelas suas reações verticais (perceba que a barra engastada terá momento fletor, pois a única reação que estamos impedindo de existir é a horizontal, todas as outras duas continuam existindo normalmente, tanto as verticais quanto os momentos, sendo assim teremos
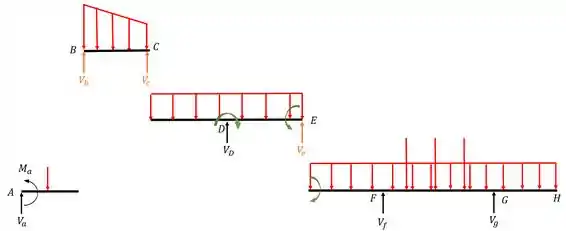
Aqui temos dois tipos de reações.
- As reações são reações fixas, ou seja, não vamos transferir para nenhum outro lugar
- As reações laranjas são reações de apoios fictícios, ou seja, iremos transferir para as barras em que esses apoios fictícios se apoiam
Dessa forma ao transferirmos essas reações dos apoios fictícios nós passamos a ter
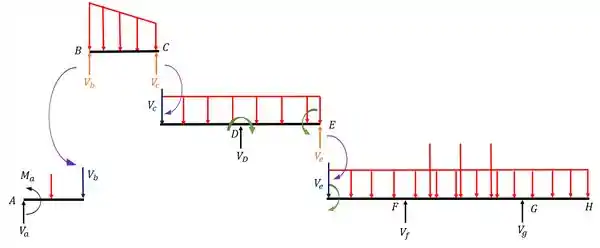
Nesse caso vemos que todas as reações dos apoios fictícios(laranjas) foram transferidas para as barras em que estavam apoiadas com o sentido invertido (cargas azuis). Ou seja, nesse ponto temos praticamente tudo separado, vamos resumir o que fizemos até agora.
- Cortamos as rótulas
- Separamos as barras
- Colocamos apoios fictícios nas rótulas cortadas
- Todas as vigas viraram vigas simples e isostáticas
- Consideramos apenas reações verticais e de momentos
- Transferimos essas cargas verticais dos apoios fictícios para as barras em que eles se apoiavam, mas com o sentido contrário.
Agora só falta a ordem de solução.
Passo 4: ordem de solução
A ordem de solução sempre será da viga mais externa, ou a que não recebe apoios fictícios, até a ultima viga a receber contribuição de outras, no nosso exemplo é a seguinte ordem.
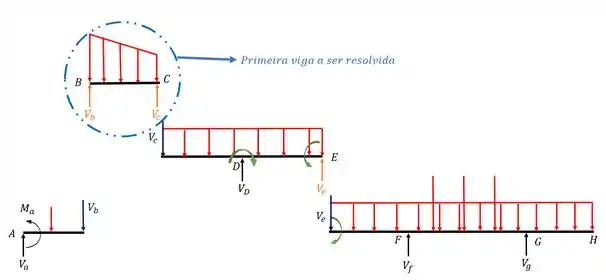
A nossa primeira viga a ser resolvida não possui apoios fictícios que se apoiam nela, e também de todas as outras vigas é a mais externa de todas, logo é a melhor viga a ser resolvida primeiro, logo, resolveremos ela completa, calculando reações de apoio, diagrama de momentos, diagrama de cortantes e tudo que for necessário ser feito para uma viga simples.
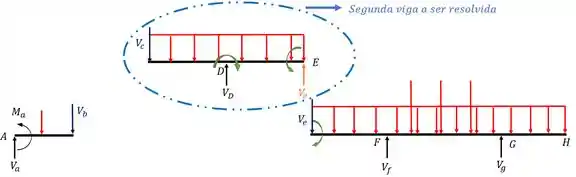
A segunda viga a ser resolvida, possui apenas um apoio fictício apoiado nela, mas que já transferimos pra ela quando calculamos a primeira viga, dessa forma ela passa a ser a viga mais externa e sem apoios fictícios nela (já que já transferimos as reações da barra BC. Novamente resolvemos ela completamente, todas as reações de apoios, diagramas de cortante e fletor, e tudo que tem direito.
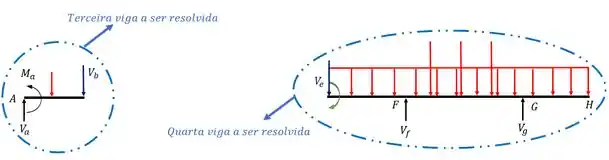
A terceira e a quarta viga já são as vigas finais, elas são as ultimas a receberem as reações de apoios fictícios, e a partir desse momento já calculamos todas as barras anteriores, logo, basta apenas calcular as reações de apoio, diagrama de momento fletor e cortante, e tudo que tem relação com vigas simples isostáticas.
Após fazer isso tudo teremos varias barras simples com diagramas de momentos fletores separados que se uniram todos na barra inicial, compondo um único diagrama de momentos fletores e cortante.
Entendido tudo isso, agora é só fazer uns exercícios para não darmos bobeira em nenhuma questão, vamos nessa, aposto que você tá doido pra fazer uns exercícios, certo?
