Teoria
Fala aí! Seja bem vindo ao Responde Aí! Bora conversar sobre treliça isostática?!
O que é uma Treliça?
Uma treliça é composta por barras, carregamentos, rótulas e apoios, que formam uma estrutura triangular. Ela é usada, por exemplo, para oferecer apoio e resistência na estrutura de uma obra e tem essa carinha aqui:
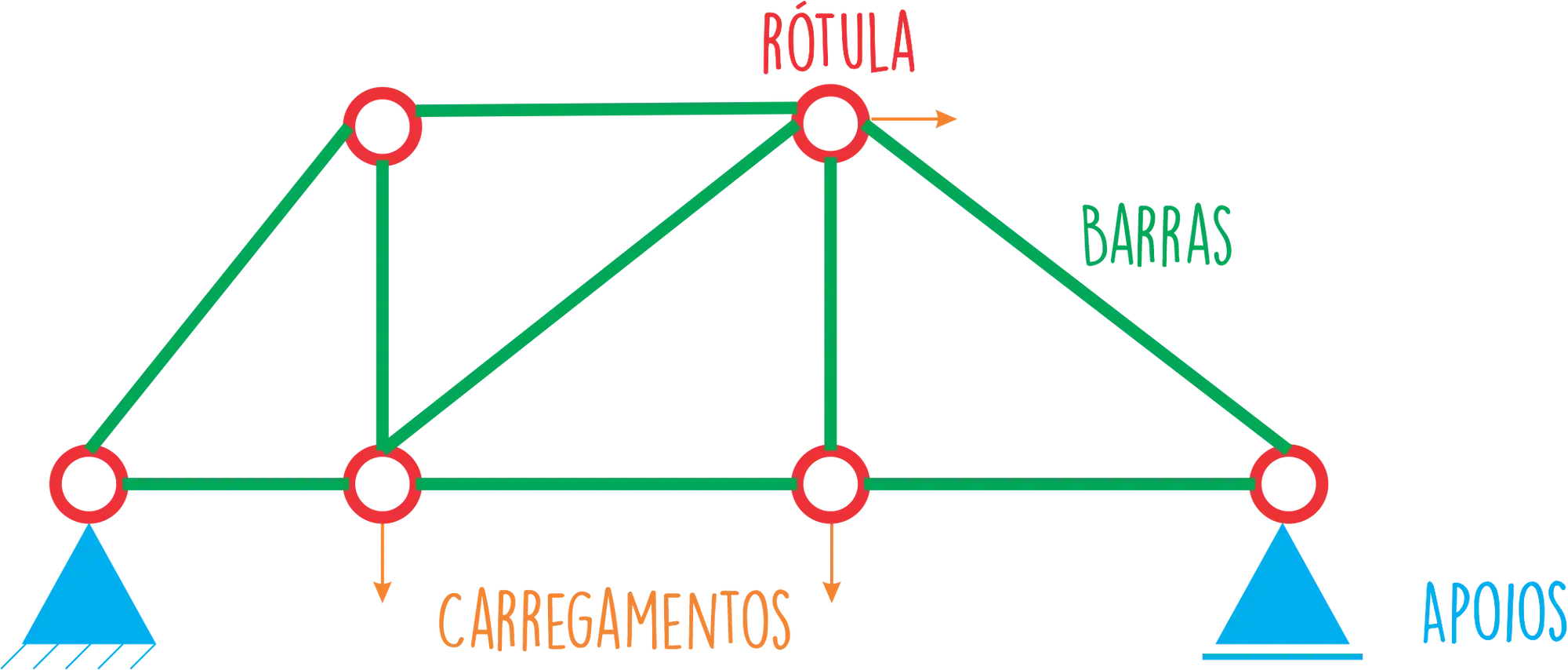
Para uma estrutura ser uma treliça ela deve ter as seguintes características:
- A treliça é composta por barras ligadas por rótulas, também chamadas de nós;
- As treliças possuem os carregamentos apenas sobre as rótulas dela, ou seja, só existem esforços normais (aqui não temos esforços de cortante e de momento fletor)
- Existem apoios agindo na estrutura da treliça.
Como saber se uma estrutura é uma treliça: Regra dos Nós
Uma treliça tem que tem SEMPRE as características que vimos ali em cima, mas pra termos certeza total de que estamos lidando com uma treliça, vamos usar a regra dos nós!
Passo 1: Escolher dois nós iniciais
Pra facilitar vamos dar prioridade aos nós dos extremos, mas é importante que sejam nós seguidos. Assim:
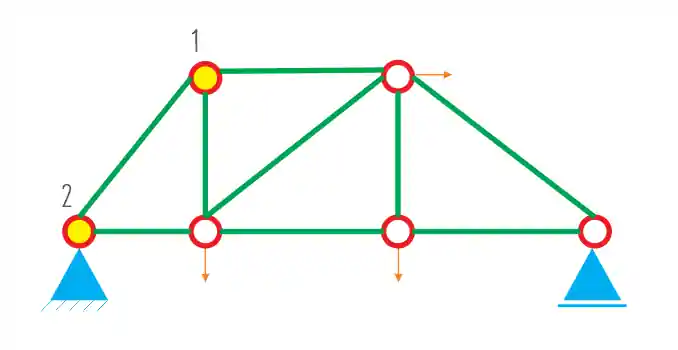
Passo 2: Chegar em um 3º nó a partir dos nós iniciais
Agora encontramos um caminho pra chegar em um terceiro nó, assim:
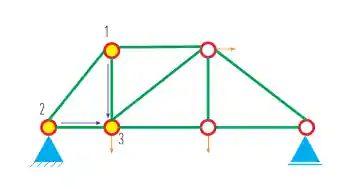
Passo 3: Repetir o passo 2 até chegar em todos os nós
Para a estrutura ser uma treliça temos que conseguir chegar em todos os nós a partir de nós anteriores, igual fizemos no passo 2. Se liga:
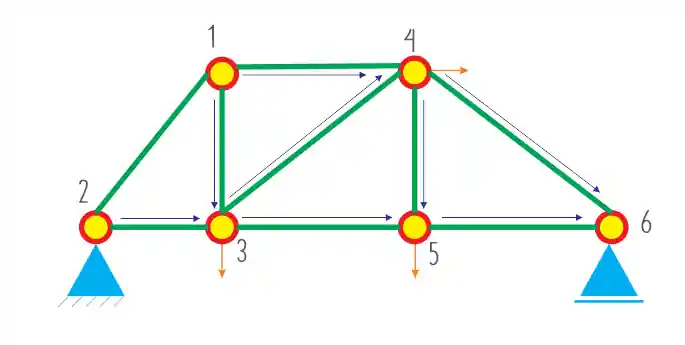
Treliça Isostática
Uma treliça isostática é formada por duas treliças simples ligadas por 3 barras não simultaneamente concorrentes ou paralelas, ou então por um nó e uma barra que não concorrem entre si.
Mas calma, na prática para descobrirmos se uma treliça é isostática, usamos a seguinte fórmula:
Onde:
é o número de rótulas; é o número de barras; é o número de reações de apoio.
Vamos conferir se a treliça do exemplo é isostática:
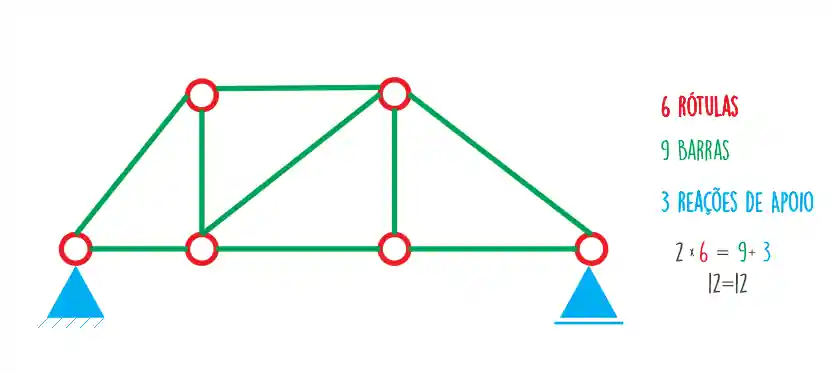
A treliça se encaixa na fórmula, então ela é isostática!
Confira também nosso conteúdo em vídeo:
Treliça Hiperestática
A treliça hiperestática obedece a seguinte fórmula:
Treliça Hipostática
Por fim, a treliça hipostática obedece a fórmula:
Agora vamos praticar com exercícios?