O vapor deve ser condensado sobre o lado do casco de um condensador com 1 passe no casco e 8 passes no tubo, com 50 tubos em cada passe, a .
A água de resfriamento entra nos tubos a com uma taxa de . Os tubos são de parede fina e têm um diâmetro de e de comprimento por passe.
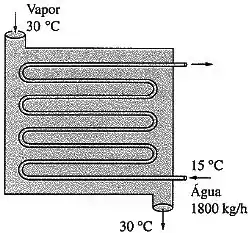
Se o coeficiente global de transferência de calor é de , determinar a taxa de transferência de calor e a taxa de condensação do vapor.
Passo 1
Determinar a taxa de transferência de calor.
Como não temos as temperaturas de saída, vamos com o Método da Eficiência e NUT. Assim, podemos calcular a taxa de transferência de calor da seguinte forma:
Vamos calcular cara um desses termos separadamente.
Passo 2
A taxa de transferência de calor máxima possível é dada por:
Como o fluido quente está passando por uma mudança de fase (temperatura constante), haverá variação de temperatura somente no fluido frio, de forma que:
Onde . Logo:
Dessa forma, a taxa de transferência de calor máxima possível será:
![]()
Passo 3
Para calcular a efetividade da transferência de calor vamos precisar calcular o NUT e a razão das capacidades .
O NUT é dado por:
Onde a área de troca térmica será:
Assim, o NUT será:
E como um dos fluidos está em mudança de fase, .
Assim, a relação para a efetividade apropriada será:
![]()
Passo 4
Finalmente, a taxa de transferência de calor real será:
![]()
Passo 5
Determinar a taxa de condensação do vapor.
Agora que já temos a taxa de transferência de calor, podemos encontrar a taxa de condensação do vapor através da seguinte equação:
Substituindo os valores:
![]()
Resposta