Para o pórtico abaixo determine o sistema de equações completo que devemos resolver para determinação dos seus esforços.
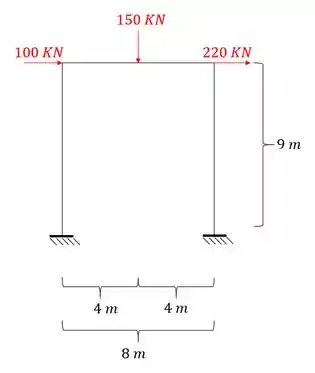
Passo 1
Para podermos saber como montar o nosso sistema, precisamos em primeiro lugar saber quantos termos nosso sistema vai ter, e já sabemos que isso vai ser dado pelo número de hiperestáticos, então o que precisamos fazer é determinar o número de hiperestáticos do nosso problema.
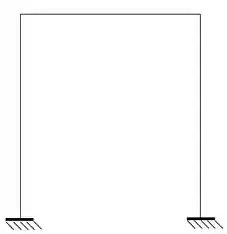
- Hiperestáticos totais pelo macete
- Sabemos que temos 2 apoios do terceiro gênero, totalizando 6 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
- Tudo referente ao ponto 1
- Tudo referente ao ponto 2
- Tudo referente ao ponto 2
Ou seja, nossa estrutura possui três graus de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática. E bem, é exatamente isso que vou fazer, e é aqui que mora o segredo, podemos quebrar qualquer vínculo da nossa estrutura, desde que ela fique isostática.
Passo 2
Nesse caso devemos quebrar 3 vínculos. Podemos sumir com o apoio central, quebrando os dois vínculos dele, e um vínculo horizontal do apoio mais a direita.
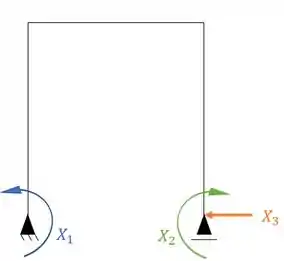
E veja que já chamei eles de X1, X2 e X3
Passo 3
O próximo passo é bem importante, porque consiste em determinar o número de sistemas que vamos ter que trabalhar, e sabemos que o número de sistemas é dado pela fórmula
Com isso fica bem simples determinar o nosso numero de sistemas, pois no passo anterior já determinamos o nosso número de hiperestático.
Com isso teremos:
Sabemos que um dos sistemas é o nosso sistema principal, ou como gosto de chamar, sistema zero, onde está o nosso carregamento.
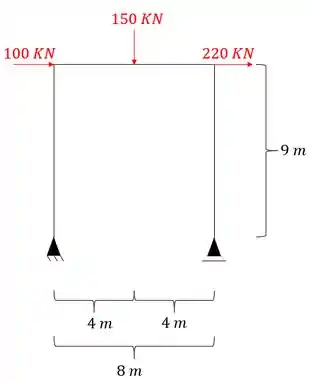
Temos o segundo sistema, que é onde vai estar o nosso hiperestático, ou seja, o nosso X1, que podemos definir da seguinte maneira:
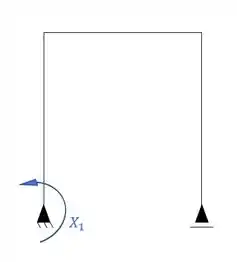
E temos o terceiro sistema, que é onde vai estar o nosso segundo hiperestático, ou seja, o nosso X2, que podemos definir da seguinte maneira:
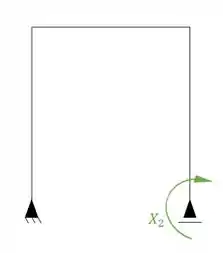
E temos o terceiro sistema, que é onde vai estar o nosso terceiro hiperestático, ou seja, o nosso X3, que podemos definir da seguinte maneira:
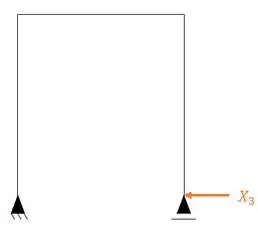
Logo em resumo temos isso aqui
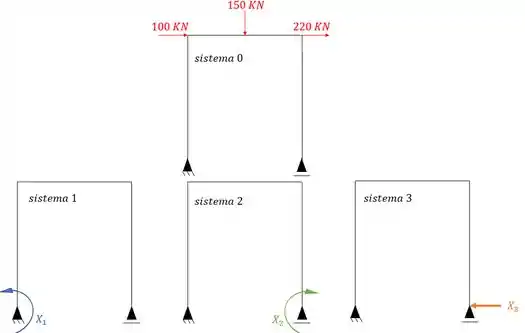
Passo 4
Agora precisamos lembrar como definir a nossa equação, sabemos que o formato segue o seguinte padrão

E sabemos que como liberamos a estrutura para se movimentar, sendo que ela não possuía esse movimento, precisamos garantir que o que ocorre no sistema 1, e no sistema 0 irão se anular, ou seja, podemos escrever que a deformação no ponto 1 e que ocorre no sistema 0 é dada pelo termo
Mas que de maneira análoga, também temos os deslocamentos no ponto 2 e 3 no sistema zero, além do mais, também liberamos o movimento no ponto 2 e 3, ou seja, também temos que garantir que o ponto 2 e 3 irá se anular na junção de todos os sistemas, sendo assim temos que:
E que a deformação que é dada no mesmo ponto 1 mas agora no sistema 1 pode ser escrito como:
e que de maneira análoga, no ponto 2 e 3 , devido o carregamento 2 e 3 , também teremos deslocamentos, mas nesse caso sabemos que o carregamento dois está no nosso sistema dois e o 3 no sistema 3, sendo assim temos que:
E por fim temos o deslocamento causado no ponto 1 devido a carga em dois e 3, e claro, o deslocamento no ponto 2 devido a carga em 1 e 3, e por fim, o deslocamento em 3 devido as cargas em 1 e 2 , que também devem ser contabilizados afim de anular o movimento.
Passo 5
E agora entra nosso pulo do gato, eu tenho que garantir que quando eu juntar todos os sistemas, tudo que ocorrer na junção dos sistemas deve ocorrer no sistema único hiperestático, e pra fazer isso eu só preciso resolver mais uma coisa. Eu sei quanto que vale porque eu tenho os carregamentos do sistema 0, mas quanto valem as outras deformações? Eu não faço ideia, mas eu sei o seguinte, se eu analisar o meu hiperestático X1 e X2 como sendo de valor unitário agindo na minha estrutura, eu consigo determinar o valor de ,para uma carga unitária, e com isso basta eu fazer a deformação para uma carga unitária, multiplicada para a carga real, que eu tenho a deformação real, que é basicamente fazer isso aqui.
E como eu abri o sistema hiperestático para um movimento que não existia, e quero que todos os sistemas funcionem iguais, eu tenho eu garantir que o conjunto seja igual a zero, ou seja:
E podemos escrever o nosso sistema como:
E assim temos o nosso sistema a ser resolvido.