Exercícios Resolvidos de Método dos deslocamentos no caso com deslocabilidade externa
Ver TeoriaEnunciado
Para a estrutura abaixo, determine o deslocamento vertical do ponto B da estrutura abaixo.
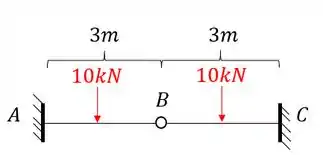
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, fazendo isso teremos que:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e C são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que o ponto B é uma rótula, logo, também não possui deslocabilidade interna.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e C são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder ir para esquerda ou direita devido o engaste em A e B, pode ir pra cima ou para baixo, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
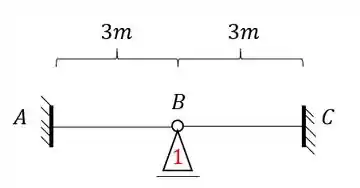
Passo 2
Como só temos uma deslocabilidade, e essa deslocabilidade é um apoio do primeiro gênero, precisamos detemirnar a reação que age nele e essa reação será o valor de .
As cargas de 10 kN que irão causar as reações de apoio, dessa maneira teremos que usar a seguinte fórmula para o caso de carga concentrada e para condições de contorno do tipo engaste e apoio.
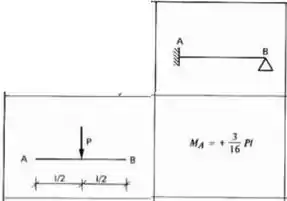
Precisamos analisar a contribuição de ambos os lados da viga:
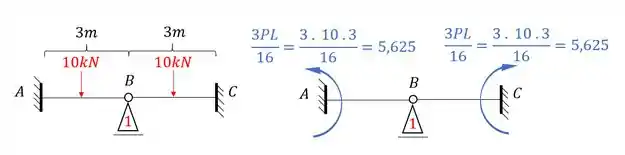
Mas lembre-se que o que importa pra gente é a reação de apoio, e não necessariamente o momento, apesar de usarmos ele para determinação da reação de apoio. Dessa maneira teremos que:
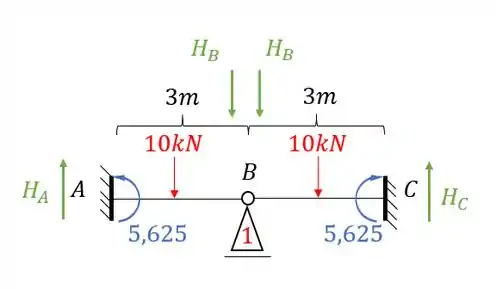
Perceba que como quem age no nosso apoio fictício do primeiro gênero em 1 é o iremos usar ele para determinar a reação do nosso apoio.
Um macete legal para lembrarmos é que o que definimos para (modulo, sentido e direção) já vai valer para a reação que age em 1. Isso é para não precisar ficar transferindo carga, ou ficar pensando se tem que inverter a direção ou o sinal.
Absolutamente não, se der pra frente a reação é pra frente, se for pra baixo a reação é pra baixo, e assim em diante. Se der negativo, a reação será negativa, gravando assim fica mais fácil de lembrar, e com isso o nosso cálculo será:
Ou seja, o nosso valor de será negativo.
Passo 3
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
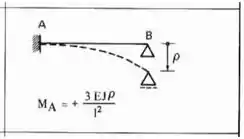
Fazendo esse deslocamento na nossa estrutura teremos que:
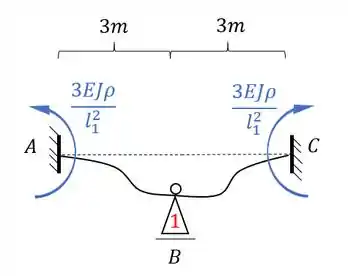
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações verticais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
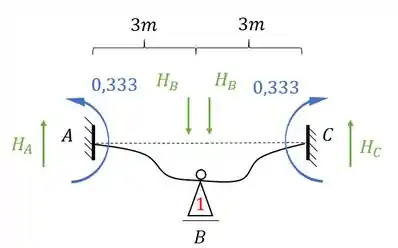
Perceba que precisamos dos valores de e . Com isso teremos que:
Como temos dois teremos no final que:
Passo 4
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento vertical do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que: