Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método dos deslocamentos no caso com deslocabilidade externa

Ver Teoria
Exercício 12345

Enunciado

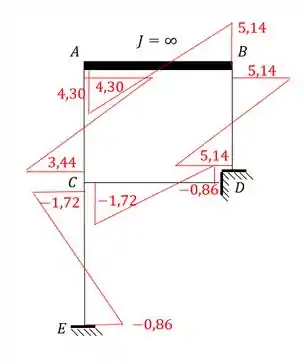
Para a estrutura abaixo, determine o diagrama de momentos fletores.

u s e   E J = 10 5

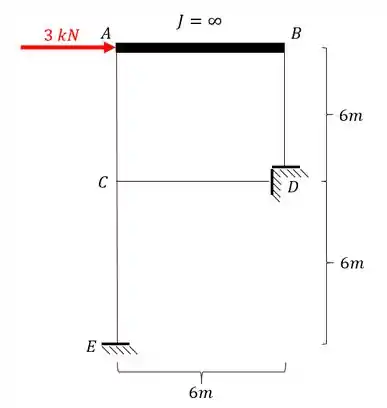
Passo 1

Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, ms nessa estrutura temos que tomar um cuidado devido a barra de inércia infinita:

  • Analisando primeiro as deslocabilidades internas:

    • Sabemos que os pontos E e D são indeslocáveis, logo, não possuem deslocabilidade interna.
    • O ponto C não é nem rótula e nem apoio extremo, logo possuirá uma deslocabilidade interna. E sabemos que se possuímos deslocabilidade interna, temos obrigatoriamente que travar ela com uma chapa, sendo assim teremos que:

    • Agora que vem o diferencial. Os pontos A e B estão nas extremidades da barra com inércia infinita. SEMPRE que tivermos uma barra com inércia infinita, ela obrigatoriamente tornará os nós da sua extremidade indeslocaveis com relação a rotação. Ou seja, os nós A e B não podem rotacionar porque a barra AB possui uma inércia taõ grande que já vai impedir isso. Ou seja, só temos 1 deslocabilidade interna.

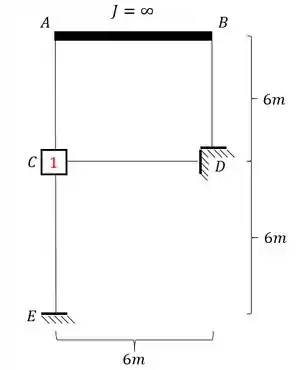
  • Analisando agora as deslocabilidades externas:

    • Os pontos E e D são engastes, logo são considerados indeslocaveis.
    • O ponto C também pode ser considerado assim, além do mais, não pode nem se deslocar pra baixo e pra cima, e nem da esquerda para direita ou vice versa.
    • O ponto B também não pode se deslocar na vertical, porém pode claramente se deslocar na horizontal, por isso devemos travar ele nesse sentido, com o nosso velho amigo apoio do primeiro gênero.

    • Com o ponto B travado podemos ver que passamos a ter o ponto A indeslocavel, logo teremos apenas 1 deslocabilidade externa mesmo.

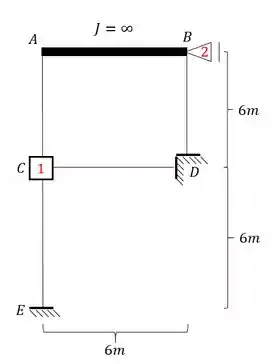
Passo 2

Sabendo as deslocabilidades e colocando os seus respectivos travamentos, agora já podemos começar a determinar as deformações do nosso problema.

Começando por β 10 e β 20 , teremos que:

  • β 10

    • Para determinação dele devemos olhar o nosso carregamento.

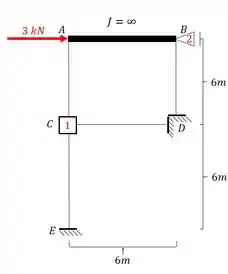
    Perceba que o ponto A assim como o ponto C são como engastes, e a carga de 3kN age bem em cima do “engaste” em A. O que isso significa? Significa que nenhuma momento será produzido, e se não tem momento sendo produzido, não temos rigidez sendo produzida em 1 devido a carga de 3kN. Sendo assim, podemos imediatamente definir que:

    β 10 = 0

    E como não teremos momento sendo produzido em nenhum nó, podemos dizer que os momentos de todos os nós analisando da perspectiva de momento em 1 será.

  • β 2 0

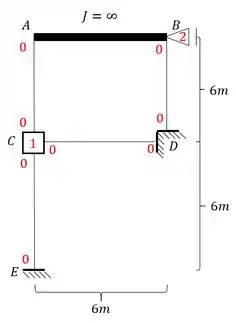
    • Para determinação dele devemos olhar o nosso carregamento.

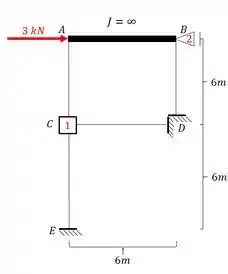
    Agora a história é outra, precisamos determinar a reação que aparece no apoio 2. Perceba que a carga de 3kN age bem em cima dele e na mesma direção, ou seja, toda a carga será transferida diretamente pro apoio. Como no calculo de β 1 0 não tivemos nenhum momento fletor calculado, então podemos ficar tranquilos, pôquer assim sabemos que não haverá nenhuma outra contribuição agindo em 2. Se por acaso tivéssemos algum momento, então poderíamos analisar a contribuição dele. Como não tem, podemos ficar bem tranquilos e analisar apenas a reação de apoio que será.

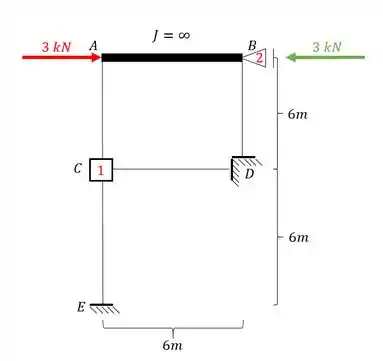
    Lembre-se que para reação de apoio consideramos para trás negativo e para frente positivo, dessa maneira temos que como a reação é para trás, consideraremos ela negativa, e com isso teremos que:

    β 2 0 = - 3

    E como toda a carga se transfere para o apoio 2, a reação de apoio em todos os outros apoios e pontos será zero.

    Passo 3

    Agora que definimos as rigidezes do sistema zero, precisamos determinar nos sistemas com a deformação de cada um dos travamentos, sendo assim teremos que:

  • β 11   e   β 21

    • Sabemos que para definir β 11 é muito simples, como se trata de uma chapa, basta rotacionarmos ela em 1 grau, que sempre rotacionamos no sentido anti-horário para sempre termos esse valor positivo.

    Como todas as extremidades são engastadas, e até mesmo os pontos A e B representam engastes, então teremos que a fórmula a ser usada é:

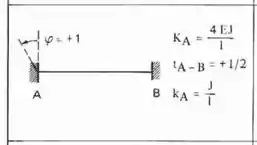
    Fazendo isso na nossa estrutura teremos que:

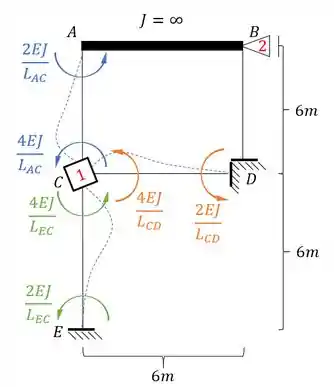
    Sendo assim o valor de β 11 será:

    β 11 = 4 E J L A C + 4 E J L E C + 4 E J L C D

    Sabemos que podemos usar rigidez relativa para facilitar as nossas contas, que podemos usar:

    1 E J

    Sendo assim teremos que:

    β 11 = 4 E J L A C + 4 E J L E C + 4 E J L C D 1 E J = 4 L A C + 4 L E C + 4 L C D = 4 6 + 4 6 + 4 6 = 2

    Para determinar o valor β 21 é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 2.

    Veja que somente as barras EC e CA produziram reações na horizontal. Porém apenas a barra CA irá interferir no nosso apoio em 2, por isso iremos calcular apenas a reação de apoio referente a ela, sendo assim teremos que:

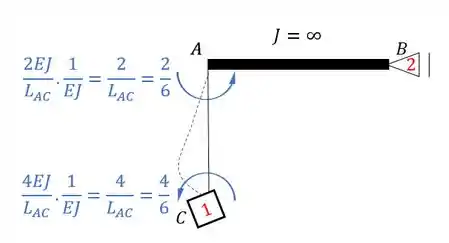
    Marcando as reações teremos que:

    - 6 H A + 2 6 + 4 6 = 0

    H A = 1 6

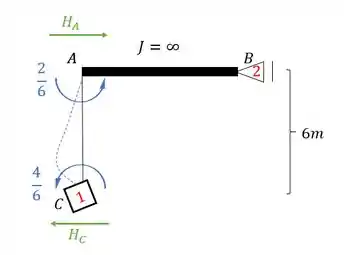
    E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se H A está pra frente, e na mesma direção do apoio 2, então a reação em 2 vai ser pra frente também e com o mesmo valor de   H A . Sendo assim teremos que:

    β 21 = H A = 1 6

    Passo 4

    Agora que definimos as rigidezes do sistema 1, precisamos determinar no sistema 2. Como o sistema 2 é um apoio iremos precisar usar o conceito de deformação e não amis de rotação.

  • β 22   e   β 12

Sabemos que para definir β 12 é muito simples, como se trata de uma chapa, basta analisarmos o momento que aparecerá nela após a deformação de 1 unidade.

Como todas as extremidades são engastadas, e até mesmo os pontos A e B representam engastes, então teremos que a fórmula a ser usada é:

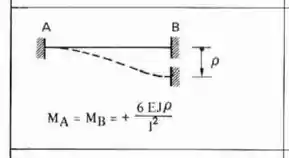
Fazendo o deslocamento na nossa estrutura teremos que:

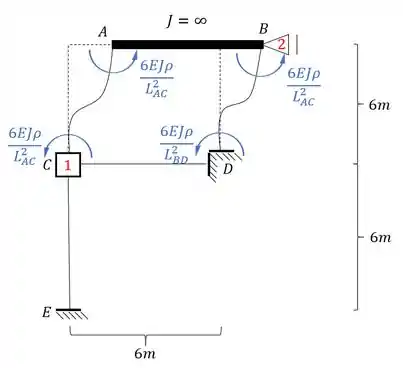
Sendo assim o valor de β 1 2 será:

β 1 2 = 6 E J ρ L A C 2

Sabemos que podemos usar rigidez relativa para facilitar as nossas contas, que podemos usar:

1 E J

E também podemos usar que:

ρ = 1

Sendo assim teremos que:

β 1 2 = 6 E J ρ L A C 2 1 E J = 6 L A C 2 = 6 6 2 = 1 6

Para determinar o valor β 2 2 é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 2.

Veja que somente as barras CA e DB produziram reações na horizontal, por isso iremos calcular apenas a reação de apoio referente a elas, sendo assim teremos que:

- 6 H A + 1 6 + 1 6 = 0

H A = 1 18

- 6 H B + 1 6 + 1 6 = 0

H B = 1 18

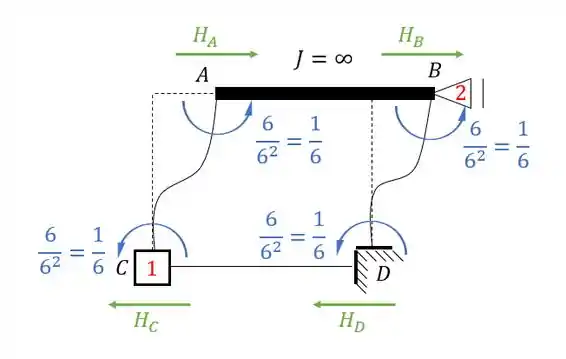
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se H A e H B   estão pra frente, e na mesma direção do apoio 2, então a reação em 2 vai ser pra frente também e com o mesmo valor de   H A + H B . Sendo assim teremos que:

β 2 2 = H A + H B = 1 18 + 1 18 = 2 18 = 1 9

Passo 3

Resolvendo o nosso sistema vamos ter que:

β 10 + β 11 ∆ 1 + β 1 2 ∆ 2 = 0

β 2 0 + β 2 1 ∆ 1 + β 2 2 ∆ 2 = 0

Substituindo teremos que:

0 + 2 ∆ 1 + 1 6 ∆ 2 = 0

- 3 + 1 6 ∆ 1 + 1 9 ∆ 2 = 0

∆ 1 = - 2,57  

∆ 2 = 30,86

Para determinação dos momentos precisamos do valor de momento fletor em cada ponto de cada sistema que analisamos, ou seja:

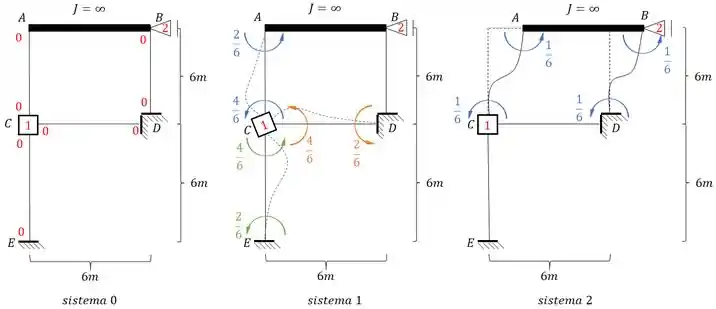
Como já determinamos os valores de ∆ 1 e ∆ 2 basta determinarmos os momentos usando a seguinte fórmula:

M = M 0 + ∆ 1 M 1 + ∆ 2 M 2

Substituindo teremos que:

M = M 0 - 2,57 M 1 + 30,86 M 2

Calculando os momentos teremos que:

M E = 0 - 2,57 . 2 6   + 30,86   .   0 = - 0,86   k N m

M C ( i n f e r i o r ) = 0 - 2,57 . 4 6   + 30,86   .   0 = - 1,72   k N m

M C ( d i r e i t o ) = 0 - 2,57 . 4 6   + 30,86   .   0 = - 1,72   k N m

M C ( s u p e r i o r ) = 0 - 2,57 . 4 6   + 30,86   . 1 6 = 3,44   k N m

M D ( e s q u e r d a ) = 0 - 2,57 . 2 6   + 30,86   . 0 = - 0,86   k N m

M D ( s u p e r i o r ) = 0 - 2,57   .   0   + 30,86   .   1 6 = 5,14   k N m

M A = 0 - 2,57   . 2 6   + 30,86   .   1 6 = 4,30   k N m

M B = 0 - 2,57   .   0   + 30,86   .   1 6 = 5,14   k N m

Fazendo o momento teremos que:

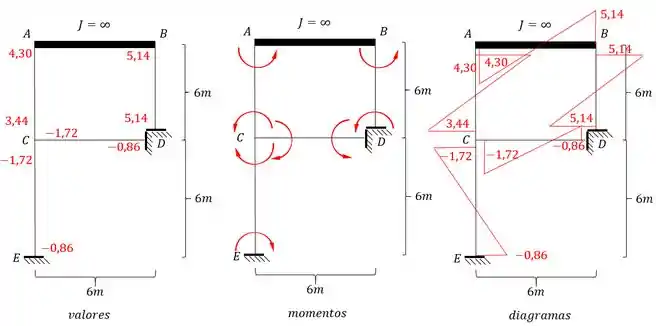
Resposta