Determine a equação diferencial matricial em variáveis de estado para o circuito abaixo. Fazer , e
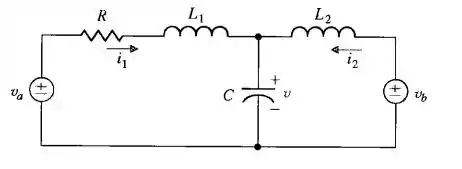
Passo 1
O primeiro passo é escrever as EDO’ que governam o sistema.
Para encontrar essas EDO’s, vamos usar a lei das malhas. Vamos escrever uma equação para a malha onde passa a corrente e outra para onde passa a corrente :
Além disso, também sabemos que a corrente que passa no capacitor é igual à soma das correntes e :
Passo 2
Para escrever a equação diferencial matricial em um modelo de estado, precisamos escrever a equação diferencial do vetor de estado que tem a seguinte forma:
Como temos três EDO’s de primeira ordem, precisamos de três variáveis de estado. Para nossa sorte, o enunciado já determinou qual será o nosso vetor de variáveis de estado:
Além disso, para esse circuito, temos duas entradas:
Vamos substituir tudo isso nas equaões , e :
Passo 3
Para escrever a equação diferencial em variáveis de estado na forma matricial, precisamos encontrar o vetor .
Rearranjando as equações , e :
Passo 4
Com as equações , e , podemos obter nosso vetor e assim, escrever a equação diferencial em variáveis de estado na forma matricial.