Usar modelo em variáveis de estado para descrever o modelo do circuito abaixo. Utilize a corrente e a tensão no capacitor como variáveis de estado.
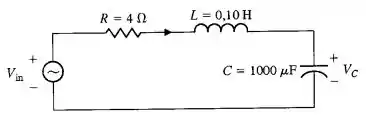
Passo 1
Vamos começar aplicando a lei das malhas no nosso circuito. Como só temos uma mlaha no circuito, só teremos uma equação:
Além disso, vamos estabelecer uma relação entre e a corrente :
Passo 2
Para escrever a EDO em um modelo de estado, precisamos escrever a equação diferencial do vetor de estado que tem a seguinte forma:
O exercício já determinou qual será o nosso vetor de variáveis de estado:
Além disso, podemos assumir que a nossa entrada será a tensão de entrada do sistema:
Sendo assim, precisamos encontrar uma expressão para as derivadas das nossas variáveis de estado.
Sunstituindo as variáveis de estado nas expressões e , teremos:
Rearranjando :
Derivando dos dois lados teremos:
Passo 3
Como já temos o nosso vetor , já podemos escrever a equação diferencial do vetor de estado:
Substituindo os valores do problema: